数学的传质
液体和气体之间的阶段,大规模的转移从一个阶段到另一个必须通过界面边界表面。叫溶质的浓度在这个表面(yj指的是气相。相应的浓度称为[xj液相。[11]和[一]只相同的溶质浓度,他们被称为不同的基础;实际上,它们是相等的。因为他们是平等的,因为界面的厚度为零,xi和易建联必须平衡彼此。
考虑吸收的过程。如果[y]在大部分气相浓度,对界面边界的驱动力是[y] -[一]和传质速率是k ([y] - [yj),肯塔基州是气膜传质系数。传质速率存在,它必须由平等平衡液膜的传质速率。液相传质速率kx ([xi] - [x]),其中kx是液膜传质系数和[x]大部分液相中的溶质的浓度。因此,肯塔基州([y] -[一])= kx ([Xi] - [x]) (9.1)
我们所知道的是,[xi]和[一]处于平衡状态。但是,实验确定这些值将是非常困难的。因此,而不是使用他们,使用[x *]和[y *],分别。[x *]是[x]的浓度将获得如果达到平衡值。通过并行推理,[y *]也[y]会达到它的浓度达到平衡值。相应的驱动力现在[y] - [y *]和[x *] - [x],分别。理解物理意义的驱动力,见图9.8。
如图所示,[xi],[一]的平衡曲线。平衡曲线之间的关系是液相中的浓度[x]和[y]在气相浓度当没有净传质之间的阶段。对于任何给定的值[x]和[y]在液态和气态阶段,分别点([xi],[一])代表了“距离”([x]、[y])将不得不“移动”来实现其均衡值同时平衡曲线。这个距离,所代表的线段([x]、[y] ^ [xi],[一]),是实际的传质推动力;
-
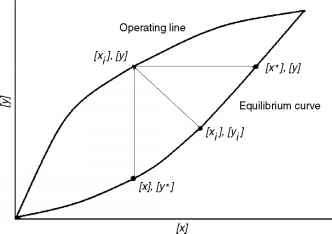
- 图9.8不同的摩尔分数之间的关系。
然而,如前所述,([xj, [yj)来确定实验是不可能的。因此,找到点([x]、[y *])来查看代理驱动力在气膜和定位([x *], [y])来查看代理在液膜驱动力。
如,[y] - [y *]大于[y] - [yj;然而,它不是真正的动力传输。也[x *]——[x] > [xj - [x],但是,它不是真正的动力传输。当传递方程,然而,前缀的比例常数。因此利用这种情况用不同的比例常数的情况下代理的驱动力。因此,使用肯塔基州的比例常数gas-side传质方程在代理情况下,肯塔基州肯塔基州(y - yi) = (y - y *) (9.2)
在流动性方面,用Kx比例常数,Kx ([Xi] - [x]) = Kx ([x *] - [x]) (9.3)
肯塔基州和Kx称为总传质系数的气体和液体,分别。区分,肯塔基州和kx被称为个人各自国传质系数。
确定相关的方程是很有意义的整体和个人传质系数。方程(9.2)可以重新获得
J_ = [y] - [y *] = ([y] -[一])+([一]- [y *] - = 1 [yj - y [*] (94)
肯塔基州肯塔基州([y] - [yj)肯塔基州([y] - [yj)肯塔基州肯塔基州([y] - [yj)
取代k ^ ([y] -[一])使用方程(9.1),
一个平行的推导Kx收益率
Kx Kx mky mky
坐标(xi)和(yi)的坐标点([xi],[一])平衡曲线。另一方面,坐标(x)和(y)坐标点([x]、[y])代表液相中的浓度[x]和[y]气体的浓度。因为阶段并不平衡,([x]、[y])不平衡曲线。的不同值对([x]、[y])的液态和气态阶段可以绘制;这个图叫做操作线(见图)。任何([x]、[y])对被称为一个操作点。操作点([x]、[y])平衡曲线上的对应点([x]、[y *])和([x *], [y]),基于代理的方程。点([x *], [y *])只能存在如果([x]、[y])在平衡曲线。
之间的斜率([x]、[y *])和([xi], [yj)([一]- [y *]) / ([xj - [x]);这等于m。因此,m是平衡曲线的斜率如果是一条直线。
平行派生可能剥离操作执行;结果是相似的。唯一的区别在于,将会有交换的下标和标。因此,以下将获得类似的方程:kx ([x] - [xi]) =肯塔基州([一]- [y]), kx ([x] - [xi]) = K ([x] - [x *])和肯塔基州肯塔基州([yJ - [y]) = ((y1 - [y])。参考图来可视化,质量流量从液相向气相。
继续阅读:心理契约的自来水多少钱
这篇文章有用吗?
