如果年代
如果S (i)是未知的,可能时间,下面的迭代估计算法可以应用(算法4.1)。只要年代(我)只需要为权重,这产生正确的估计也只有S (i)的相对变化,而不是绝对值,估计。类似地,如果S(我)只需要对权重和已知常数,然后方程式。可以使用(4.5)和(4.6)和S (i) = 1, i = 1,……,n和W = n。这个估计没有权重称为普通最小二乘法(OLS)。古典建筑的CIs(4.1.4节),然而,估计年代(i)必须是可用的。
一步 |
1 |
让最初的猜测,S (0) (i)的变化。 |
一步 |
2 |
估计回归参数,/ Jq0) / 3(0),使用的猜可变性而不是在方程式(i)。(4.5),(4.6)和(4.7)。 |
一步 |
3 |
计算e (i) = x (i) - / 0 - 31 t(我),我= 1,……,n。e(我)被称为未加权回归残差。 |
一步 |
4 |
获得一个新的变化估计,年代从残差(1)(我)。这个可以nonparametrically平滑(例如,运行标准偏差的e (i))或拟合参数模型(S)(我)e (i)。 |
一步 |
5 |
去第2步使用新的,改进的变异估计直到回归估计收敛。 |
算法4.1。线性加权最小二乘回归,未知的变化。
算法4.1。线性加权最小二乘回归,未知的变化。
4.1.1.1例子:北极河径流
气候模型raybet雷竞技最新运行自然迫使只有(图4.1)不表现出从零斜率明显不同。(参见4.1.4节的决心回归标准错误。)人为和自然相结合的运行迫使(图4.1 b)显示径流显著上升趋势。吴邦国et al .(2005)推测,可能有一个变点在1965年左右,当斜率发生了变化。
n 2
3000年
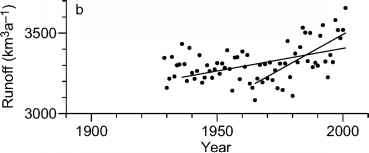
图4.1。线性回归模型拟合模拟北极河径流(图1.9)。一个自然强迫只;b结合人为和自然强迫。吴et al .(2005)后,符合(实线)通过OLS回归使用数据从整个区间1900 - 1996 (a)和(b)两个区间,1936 - 2001和1965 - 2001。估计回归参数(方程式。4.5和4.6)和标准错误(方程式4.24和4.25)如下。英尺= 3068±694 km3a-1,英尺= 0.102±0.356 km3a-2;b 1936 - 2001英尺= -2210±1375 km3a-1英尺= 2.807±0.698 km3a-2;b 1965 - 2001英尺= -13977±3226 km3a-1 km3a-2英尺= 8.734±1.627。
图4.1。线性回归模型拟合模拟北极河径流(图1.9)。一个自然强迫只;b结合人为和自然强迫。吴et al .(2005)后,符合(实线)通过OLS回归使用数据从整个区间1900 - 1996 (a)和(b)两个区间,1936 - 2001和1965 - 2001。估计回归参数(方程式。4.5和4.6)和标准错误(方程式4.24和4.25)如下。英尺= 3068±694 km3a-1,英尺= 0.102±0.356 km3a-2;b 1936 - 2001英尺= -2210±1375 km3a-1英尺= 2.807±0.698 km3a-2;b 1965 - 2001英尺= -13977±3226 km3a-1 km3a-2英尺= 8.734±1.627。
4.1.2广义最小二乘估计
在实际的气候环境中,Xnoise (i)通常展品持久性。这意味着结构或信息内容超过一个纯粹的随机过程。这些知识可以用于应用广义最小二乘估计(gl),下面的平方和最小化:
在此,
(参数向量),
(数据向量),
(时间矩阵)
V是一个n * n的矩阵和协方差矩阵。解决方案是gl估计量,()
gl的优势提供回归估计的标准误差小于WLS的持久性。类似地,在时间的情况下(我),WLS估计比OLS估计(森和斯利瓦斯塔瓦1990)。协方差矩阵r 1的元素。
V (il, i2) =(2)■年代(i2)■E [Xnoise (il)“Xnoisefe)]
i1、i2 = 1…,n。气候实践通常需要估计除了可变性也持久性(第二章)获取V矩阵。在不均匀间隔的AR(1)持久性模型(Eq。2.9),唯一未知除了年代(i)所需计算V是持久性,t。估计V矩阵元素
V (il, i2) =(2)■年代(i2)■exp (- | t (2) - t (i2) | / r /;
i1、i2 = 1…n, r是估计,bias-corrected持久性时间(2.6节)。甚至间距,取代指数表达式(的)| il-i21。(在持久性比AR(1)模型更复杂,V是可计算的,因此,gl只适用于均匀间隔的时间序列)。自相关或持续时间估算公式(方程式2.4和2.11)应用于加权WLS回归残差,r (i) = [x (i) - V - Mi) / S(我)
我= 1,……,n。消除趋势由线性回归是不一样的意思是减法,和自相关的偏见和坚持时间估计不需要遵循近似给出平均减法(2.6节),但是是未知的。然而,和其他不确定性偏差可能微不足道。还在未知的持久性,迭代过程类似于WLS可以应用,被称为广义最小二乘估计(egl)(其中森和斯利瓦斯塔瓦1990:7.3节)。4.1.4.1节给出了一个egl程序的AR(1)持久性。
4.1.3其他类型的估计
最小二乘(OLS、WLS gl)是一种符合标准。另一个原因是最大似然(2.6节,58页)。进一步的标准结果进一步偏好的回归过程。一个显著的选择是鲁棒性对异常数据的影响,Xout(我)。这可以通过最小化的平方和(Eq。4.4),广场的中值,m {[x (i) - fto ft1t (i)) 2 / S (i) 2} J =我。(4.17)
最好(背景材料)是削减平方和最小化,n-j
SSQT (fto, ft1) = E [x”(i) - fto ft1t“(我)]/ S”(i) 2(4.18)我= j + 1
j = / NT (5 n) / NT(■)是整数函数,0 < 5 < 0.5,x”(i)是size-sorted x(我)和t (i)和S”(i)是“奴隶”,相应的重新安排。修剪排除了2 j极端条件导致了估计。同样的总和最小化的绝对偏差,n
SSQA (fto ft1) = E \ x (i) - fto ft1t (i) | / S(我),(4.19)
离群值(如果不是已经排除了通过之前的分析)可以少比最小二乘回归估计影响最小化。这样的标准也可能是可取的(而言,标准的错误估计)而不是Xout时最小二乘(我)我们认为重尾分布或倾斜Xnoise (i)分布。
到目前为止介绍的各种标准和相关的最小化技术代表了计算方面的回归估计问题。第二,或许更相关的方面是线性回归模型的适用性。在气候学,这意味着一个线性是否增加或减少不太简单描述Xtrend (T)。通过各种模型适用性可以评估图形类型的情节回归的残差(Eq。4.16)。这些噪声过程的实现应该名义上没有表现出比假定的持久性模型结构。
4.1.4古典置信区间
假设一个数据集{t(我),x (i)} rn = 1以下假设:
1。Xnoise高斯形状(我);
2。协方差矩阵V (Eq。4.14),包含持久性和变化特性,正确估计;
然后为gl估计CIs(30和“/ 31 Eq。(4.13)可以由学生的t分布(森和斯利瓦斯塔瓦1990):
CI0j, 1-2a f3j +是从(a)■se ^。足总+是从(1 - a)■se ^。(4.20)
j = 0(拦截)和1(坡)。估计的标准误差(森和斯利瓦斯塔瓦1990)
继续阅读:Sejj [Cjj12 421
这篇文章有用吗?