在平面应变不变量
现在让我们来研究一下在平面应变不变量之间的关系(方程(9.5))和方程(9.8)。通过平面应变我们意味着没有变形的一个坐标方向,在这种情况下,z。是由偏应力引起的变形,这意味着aZz, 'xz, ^ 0。从方程(9.7)我们因此有:
所以azz = P,然后从方程(9.6):
(注意,因为azz = P, azz不等于0,即使'zz。)与azz = 0, j - 1 = ('xx + ay,)。利用方程(9.7)和(9.13),然后容易显示,在三维空间中,j - 1也在平面应变= 0。
然后从方程(9.10),加减2 'xxa 'yy完成广场:
J2 = 2 K + 2 axy + * + 2 'xxa 'yy - 2 a 'xxa 'yy)
J2 = 1 ((“„- 'yy) 2 + 2 % + 2„ayy]
改变总压力用方程(9.7),那么收益率:
J2 = 1 ((axx - ayy) 2 + 2 axy + 2 ^ ayy - axxP ayyP + P2)]经过一些操作使用方程(9.13),我们得到:
2 ((axx - ayy) 2 + 4 ? y]
(它可以:表明J3 = J2在二维空间中,但是我们不会这样做。)
你会认识到右手边的方程(9.13)和(9.14)作为不变量的方程(9.5)和(9.5 b),分别。使用方程(9.9)你会发现| (axx + ayy) = 3 h和
-
- rOSLdx dx
^ dx pgdxdydz
^ dx pgdxdydz
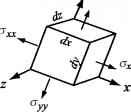
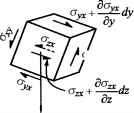
图9.5。压力在一块大小dxdy dz。(一)正常压力。(b)剪切应力(仅在x方向上)。
从方程(9.14)±[(a22 - ayy) 2 + 4 ^ y) 1/2 = VJ =所以我们首次发现的不变量方程(9.5)两个维度I1和J2的函数。
方程(9.14)的右边是平面应变的最大剪应力。可以通过设置显示的微分方程(9.2)= 0。如果轴,另外,选择主应力平行,a2y会消失,离开:
最大剪切应力的方向将45°、135°轴。(显示这个,确定方向的飞机最多,使用过程类似于我们用来获取方程(9.3),并比较这些飞机与飞机的方向,一个是最大的)。
继续阅读:冰川下的水管道
这篇文章有用吗?
