Rdp
K = (u2 + v2) / 2是动能和gh是重力势能。通过集成(25)在整个极域,得到d ~ dt ff (K + gh) rdr dp = 0,
这表明总集成能量是守恒的。在一个集成的意义上,重力势能的变化必须平衡等于动能的变化。乘以r -(2)和重写使用绝对角动量M =房车+ / r2 2(或空运的角动量由于涡和地球自转)我们获得绝对的角动量原则
方程(27)表明,绝对的角动量是物质守恒的缺席的方位扭矩gdh / dp。这一原则有深刻的影响飓风动力学。在飓风,径向压力梯度力国民幸福指数/博士比方位压力梯度力大得多(g / r) dh / dp,经常米几乎是物质守恒的边界层的飓风。边界层中存在摩擦,这样空气包裹内螺旋他们失去了角动量。附近材料M表明任何保护机制,能够移动空气径向向内较小的半径也将导致切向风速增加,同样的空气会导致切向风速呈放射状向外移动减少。这是类似于图滑冰运动员当他或她的手臂旋转的更快带来内在的,反之亦然。此外,非对称对流可以创建方位扭矩变化m .因此,一个空气包裹,螺旋向内有利的方位扭矩从非对称对流可以迅速增加其绝对的角动量。
2.5 Eddy-mean流相互作用
在前面的部分中,扰动被认为是小相比,他们的手段,这允许我们忽略了高阶项。然而,在许多情况下,PV不对称是足够大的大小线性模型不再有效。从这个意义上说,“波”一词应该替换为更普遍的术语“艾迪”,和涡流在非线性方面的交互可能意味着漩涡。例如,在某些位置涡流可能向下的平均涡在其他位置向上平均涡。
eddy-mean流相互作用可以使用的等熵公式描述优雅安德鲁斯(1983)和安德鲁et al。(1987)降低到我们的单层浅水液体。径向风u,质量加权方位一般被定义为u =胡锦涛/ h。从普通的平均偏差定义为v = v - v,和偏离质量加权平均被定义为u * = u -美国类似的定义保持其他变量。
()应用到每一项(5)和指出,胡锦涛=提升,我们可以把方位意味着质量连续性方程
dt rdr
同样,应用()在(24)和每一项指出hPu = hPu + hP *你*我们可以把方位意味着v方程dv
现在考虑径向动量方程。因为(28)和(29)包含uu,我们想(23)转换成uu的预测方程。这需要把(23日)之前方位平均通量的形式。因此,结合(23)和(5),我们获得流量形式(胡)d (rhuu) d (hvu) v, dh n
“V + w2 + ~ 7) = (30)
方位(30)的平均水平,我们获得
指出了=,huu = u hiiii +胡* * h (dh /博士)= h (dh / dr) + h ' (dh /博士)和使用方位的意思是连续性方程(28),我们获得对流形式(32)。收集上面的结果,我们得到完整的方位是方程
VU ir v \ dh vt-V + 7) * + * =: F '
在哪里
Vt rdr
方位的意思是物质导数,M =房车+ jfr2方位意味着绝对的角动量,何地
是eddy-induced有效径向和方位部队每单位质量。通过检查这些方程,它是直接清楚涡流与平均流量交互。平均径向动量可以修改eddy-induced力F和角动量的意思是可以改变的rG eddy-induced力矩。
2.6数值模拟
章节3.1和3.2中给出数值模拟得到使用/平面pseudospectral浅水模型中,笛卡尔配方的方程(3)- (5)。获得的数值解是在600公里使用512 x 512 x 600公里双周期域等距的点。dealiasing后二次平流项(3)-(5),保留傅里叶模式的数量是170 x 170,产生的有效分辨率3.52公里。三阶Adams-Bashforth时间计划使用5 s的时间步。数值扩散项添加到右边的笛卡尔形式的(3)-(5),系数v = 100平方米s - 1。科里奥利参数/ 4 = 1 x打败s - 1和平均流体深度h = 4077。3.3节中给出数值模拟进行使用nondivergent笛卡尔极限公式(3)-(5),即(3)结合V2 ^ = Z。
3所示。内部动力过程
在本节的动力学模型和关联原则是与观测结合使用来说明正压方面的重要内部动力过程负责飓风结构和强度可变性:螺旋雨带,不稳定和眼睛和眼壁之间的混合,同心眼壁周期。
3.1螺旋带
热带气旋最distiguishable特性之一是螺旋雨乐队。如果螺旋雨带被认为是小振幅扰动传播基本状态漩涡,我们可能期望线性波理论可以解释某些方面的结构和传播速度。早前视图(栗原市,1979;威洛比,1978)是螺旋带inertia-gravity波。为了说明螺旋乐队可能被视为传播inertia-gravity波,我们假设d (°/ = dh / = 0博士和一个恒定的角速度Co(13) -(15)获得ai + ^) vV + 9 = o 08)
假设可分离的解决方案形成h的(r,泰,t) = h (kr) exp(我(mty - vt))(和类似的定义保持其他变量),一个常微分贝塞尔方程得到控制的径向结构波。向外传播解这个方程是汉克尔函数H ^ (kr),用贝塞尔函数的Jm (kr)
和诺伊曼函数Ym (kr) Hjm \ kr) = Jm (kr) + iYm (kr)
(x ' (r, tyt) \ hn(我(v - Cm) \ (1)
\ h”(r,泰,t) J hk2 \ -hk2 / ho)
h0在哪一个任意常数,径向波数k和频率v(16)是相关的。相对涡度和散度与streamfunction和速度势(7)
年代(r,泰,t)) = ho(我(v - am) / - h) Hw (kr) e”(mty-vt) (42)
z (r,泰,泰= h0 \ (f + 2 co) / h)嗯(kr) e (42)
从微扰(6)我们发现径向速度u ' = (dx / dr) - (dty / rdty)和微扰方位速度v”= (dx / rdty) + (dty /博士)可以写成的u (r, < p、t) \ _日后iv”{r (p t)) ~ W
(v - m + f +领导)(m / r) H (m ^ (kr) \ - (f + la) kHm_ !(kr) y,我们使用汉克尔函数的导数关系dH ^ ^ = kHm博士(kr) / (1) t (kr)——(m / r) Hjm ^ (kr)。方程(41)——(43)consititute准确的解析解(38)-(40)表面上传播圆柱波。
在图拉,一个大的螺旋雨带在飓风亚历克斯1915 UTC,显示如图磅的线性解和h”(r, ty)显示功能向量u ' (r, ty)和一个)
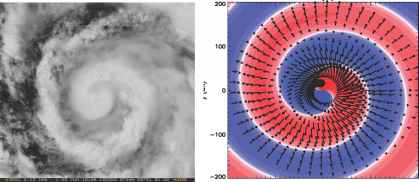
图2所示。面板:a)观察到的大型螺旋雨带飓风亚历克斯1925 UTC 6月29日,2010(左面板),b)线性解h的功能向量u和v的浅水方程在极坐标空间。使用的常量是h = 4288, cc = 5 x 10 ~ 4 s - 1, k = 4 x 10 ~ 5 m - 1, f = 3.7 x 10 ~ 5 s - 1, ho = 10 m和m = 1。向量是绘制在该地区30公里< r < 200公里。面板)是由NOAA / NESDIS / RAMMB柯林斯堡有限公司,美国。
图2所示。面板:a)观察到的大型螺旋雨带飓风亚历克斯1925 UTC 6月29日,2010(左面板),b)线性解h的功能向量u和v的浅水方程在极坐标空间。使用的常量是h = 4288, cc = 5 x 10 ~ 4 s - 1, k = 4 x 10 ~ 5 m - 1, f = 3.7 x 10 ~ 5 s - 1, ho = 10 m和m = 1。向量是绘制在该地区30公里< r < 200公里。面板)是由NOAA / NESDIS / RAMMB柯林斯堡有限公司,美国。
v ' (r, 0),红色区域表示积极h”(流体深度略高)和蓝色区域表示- h”(流体深度略低)。在这个特殊的瞬间亚历克斯像线性解决方案的大型螺旋雨带与方位浅水方程波数m = 1。注意扰动风高度发散,风的方向和散度模式对扰动的高度场有利于向外传播的波。低水平收敛可以创建一个传播的螺旋地区浅或深对流活动类似于亚历克斯的观察。然而,为了确保观察到的波的频率,线性理论需要比较。
另一个观点是,螺旋带涡罗斯比波(麦克唐纳,1968;Guinn &舒伯特,1993;蒙哥马利& Kallenbach, 1997;陈和邱,2001)。他们的论点是基于事实,螺旋带通常观察到传播方位慢于平均流量,以及乐队变得更严格的径向向外移动,类似于PV细丝。由于涡罗斯比波局限于生活的地方存在一个径向PV梯度,径向向外传播可以不再继续一旦电波传播某种停滞半径。在这个时候,在早些时候,使对称旋风倾向于剪切波的影响紧密缠绕螺旋。最终波浪衰减和axisymmetrization完成。
使用2.5节中描述的数值模型,模拟运行最初椭圆光伏领域。飓风有时会观察到有明显的椭圆形状的内核(郭et al ., 1999;Reasor et al ., 2000)。在极坐标下,在指定的初始涡度场(p) = [(1 - e2) / (1 - e2cos2(^))) 1/2是椭圆的椭圆率增强因子(x / a) 2 + (y / b) 2 = 1(其中一个是半轴长半轴和b)与离心率e = (1 - (b2 / a2)) 1/2。佐薇是最大涡度中心,f \ (r) = exp (- (A / r) exp (1 / (r ' - 1))] isamonotonic形状函数过渡陡度参数,r ' = (r - ria。(< p)) /(火箭(< p)——一种音乐形式(< p))是一个无量纲半径、ri和ro半径的涡量开始减少和消失,分别。的特殊情况(p) = 1场轴对称。实验,佐薇x三年代= 2.0 = 3.0,e = 0.60,国际扶轮和ro设为10公里,110公里,分别。平衡质量领域是由解决非线性平衡方程和初始域散度到处都被设置为0。
在图3中,螺旋雨带在雷达图像显示为雨果飓风(1989)登陆在查尔斯顿,南卡罗来纳。在图3 b中,螺旋雨带飓风丹尼尔(2010)所示的可见的卫星图像。注意,在这两个面板,螺旋带紧紧包裹,或有更大的径向波数。图3 c描述了P = (h / h)的演化数值模拟(f + Z),表示更大的PV和鲜艳的颜色。第一个面板是初始条件和后面的面板都是1.25 h。随着椭圆使对称,两个光伏细丝是可见的。这些光伏细丝是涡罗斯比波打破anticyclonically由于漩涡的旋转风以外的半径最大的风,和类似于紧缩螺旋乐队中观察到真正的飓风。最终椭圆光伏领域使对称轴对称磁单极子。在真实的氛围,垂直和水平剪切等外部因素以及内部流程如对流活动可以激发涡旋罗斯比波。对于单调漩涡,这些电波通常会随时间衰减,建立螺旋PV细丝像螺旋乐队。 As stated earlier, while inner spiral rainbands are likely sheared vortex Rossby waves, the outer bands may often be outwardly radiating inertia-gravity waves. Guinn and Schubert (1993) also hypothesized that the outer bands may form during a combined barotropic-baroclinic instability of the intertropical convergence zone. In this sense, the large PV filaments formed from this breakdown are breaking Rossby-like waves, but not vortex Rossby waves. There is continuing debate on the net effects of spiral rainbands on TC intensity. In a forced context, where the effect of deep convection are parameterized by region of enhanced PV, vortex Rossby wave theory indicates that axisymmetrization of PV anomalies (Carr & Williams, 1989) will spin-up the mean winds as the waves propagate radially outward (Montgomery & Kallenbach, 1997). In an unforced context (as described here), the anticyclonic wave-breaking outside the vortex core actually spins down the vortex winds there. The real atmosphere is much more complicated. Since spiral bands have diabatic heating, there can be associated downdrafts and subsidence in between successive bands. The spiral bands can also cut off inflow into the core of the vortex, resulting in potential weakening (Barnes et al., 1983). Further research is certainly warranted on the net effects of spiral bands, either generated by vortex Rossby or inertia-gravity waves on hurricane intensity.
3.2眼壁过程
强烈的眼壁或加强飓风经常观察到的是一个环形高架塔潜在的涡度(Kossin & Eastin, 2001;穆勒和史密斯,1994),从表面延伸到大约8 - 12公里的高度。因此在任何垂直水平方位的径向梯度意味着光伏变化从漩涡中心的边界标志。这满足Charney-Stern动态不稳定的必要条件。在三维大气,这部分是由于正压和不稳定
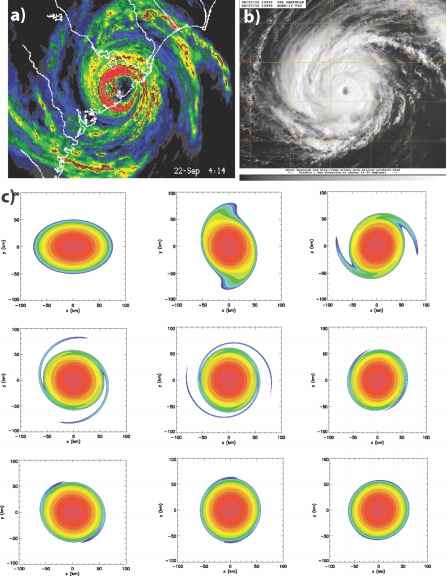
图3所示。板:1)螺旋雨带在雨果飓风登陆时9月22日,1989年在0414 UTC, b)螺旋雨带在可见的的卫星图像2010年8月23日,飓风丹尼尔。c)进化的椭圆光伏领域浅水模型。第一个图是初始条件和每个后续图1.25 h。面板(a)和(b)是由NOAA / AOML /飓风研究部门美国佛罗里达州迈阿密的。
图3所示。板:1)螺旋雨带在雨果飓风登陆时9月22日,1989年在0414 UTC, b)螺旋雨带在可见的卫星图像飓风丹尼尔在8月23日,2010年。c)进化的椭圆光伏领域浅水模型。第一个图是初始条件和每个后续图1.25 h。面板(a)和(b)由NOAA / AOML /飓风研究部门在迈阿密,佛罗里达州,美国。
斜压不稳定,前者被归因于不稳定的大型径向剪切切向风以及曲率涡度,而后者不稳定被欠的垂直切变涡切向风。我们将集中在正压不稳定和随后的眼壁和眼睛之间的混合过程。
图4所示。板:1)旋转的漩涡的眼睛MODIS的飓风伊戈尔(2010)观察到,和b) wavenumber-4模式雷达反射率在飓风多莉接近德州海岸1052 UTC 7月23日,2008年。面板)是由美国国家航空航天局和面板b)是由国家气象局在布朗斯维尔,TX,美国。
在图4中,显示两张图片来说明一些观察到的内核不对称和eye-eyewall混合在飓风。在图4中,旋转的漩涡在低水平的眼睛观察飓风伊戈尔所示,在图4 b中,wavenumber-4模式显示了飓风多莉(2008),因为它靠近南部的德克萨斯州。多边形眼壁形状,和眼睛mesovortices假设了舒伯特et al。(1999)都是一种内在的混合过程的一部分的眼睛和眼壁之间发生飓风眼壁的动态不稳定性产生的光伏中空塔。
正压不稳定在一个圆形涡是最好的理解考虑两counter-propagating涡罗斯比波之间的相互作用。考虑一个高架环涡度如图5所示。第二节所示,当地的方位相速度扰动涡度
现在考虑两个罗斯比波存在内部和外部边缘的涡环在图5中。内心的波动,dZ /博士是正的,而对于外波,dZ /博士是负的。根据(46),内波的角速度比涡动角速度,虽然外波比涡动角速度较小的角速度。因此,内波进积相对于其本地流,和外波都相对于其本地流。自从角速度概要文件为这枚戒指有一个最低的位置第一个基本状态涡度梯度,以及

图4所示。板:1)旋转的漩涡的眼睛MODIS的飓风伊戈尔(2010)观察到,和b) wavenumber-4模式雷达反射率在飓风多莉接近德州海岸1052 UTC 7月23日,2008年。面板)是由美国国家航空航天局和面板b)是由国家气象局在布朗斯维尔,TX,美国。
相应的地方波角相速度
1 dZ /博士
1 dZ /博士
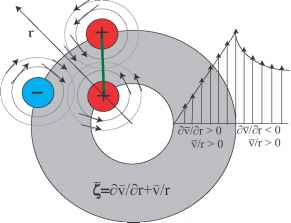
图5所示。概念模型的交互counter-propagating涡罗斯比波环的涡度升高。气旋性涡度异常积极的迹象表明,负号表示anti-cyclonic涡度异常。这个时候内外涡度异常锁定在阶段(厚绿线)upshear倾斜,每个异常和循环用平流输送其他异常,导致失真的最初轴对称戒指。
图5所示。概念模型的交互counter-propagating涡罗斯比波环的涡度升高。气旋性涡度异常积极的迹象表明,负号表示anti-cyclonic涡度异常。这个时候内外涡度异常锁定在阶段(厚绿线)upshear倾斜,每个异常和循环用平流输送其他异常,导致失真的最初轴对称戒指。
最大值的位置,第二个基本状态涡度梯度,有可能这两个波锁相,或有相同的绝对绝对角速度。如果海浪扰动涡度倾斜upshear成为锁相,如图5所示,每个异常都是在与其他交互的最佳阶段,最终导致变形的轴对称戒指。尤其要注意气旋环流与外涡度相关异常是用平流输送内内异常(反气旋异常增强的旁边),而内部的循环涡度异常是用平流输送外异常呈放射状向外。显然,涡度异常的相互作用是提高薄环和环的涡度较大的基本状态。数学上严格的描述这些counter-propagating涡罗斯比波之间的相互作用的核心是由舒伯特et al。(1999)。有趣的是,这正压不稳定也可以存在于外部区域的热带气旋(彭et al ., 2008),影响其外部结构和强度。
在正压不稳定的早期阶段,内部和外部涡罗斯比波随时间呈指数级增长。e-folding的次数后,无穷小扰动增长显著振幅的线性化方程不再有效。现在的流程是由非线性PV方程(8),平流项的主要意义。为了理解合成涡结构和强度变化产生的正压不稳定,我们必须使用一个数值模型来模拟光伏平流。在真实的氛围,也存在扩散,可以认为是一个参数化的涡流粘度系数假设通量梯度理论。这个新的光伏方程dP d (rP) vdp
继续阅读:Dt rdr r dp
这篇文章有用吗?