盆地规模湖面驻波运动

在一个分层的分层界面波

横向模式稳定风停止和表面应力状态时放松,与相关的重力复原力的冠军d接口(水面或温跃层)变得不平衡。可用势能体现在重力作用下的倾斜释放和转化为动能的接口形式的正弦振荡驻波假潮。波腹被发现在盆地端墙和在盆地内部节点点(图2和5)。湖面通常称为线性波因为进化中的波场在时间和空间中描述得很详细的线性波动方程d ^ n dt2”

^ (x, t)是线性浅水相界面位移和速度(波峰和波谷)传播的速度。这个方程也同样适用于界面上自由表面波或温跃层运用适当的形式的有限公司= y ^人造石铺地面或co . = \詹h1h2 / H,表面和内部湖面波动的情况下,分别。由于重力的作用相对于自由表面在温跃层(g的^ g),表面波旅行~ 50倍的速度内波。

熟悉的驻波模式与湖面形式是对称的进步的浪潮振幅和波长,相等,但方向相反的符号,传播从upwelled downwelled流体卷两端的盆地(图2)。这些波通常用余弦函数(图5)表示,中央节点(s)和波腹盆壁。求和余弦o c

波腹

X / 2节点

波腹

波腹

X / 2节点

波腹

波腹

波腹

波腹

波腹

波腹

波腹

波腹

波腹

波腹

波腹

波腹

波腹

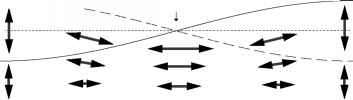
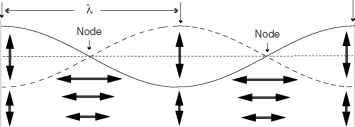
图5原理图显示前三个水平界面湖面波动模式:横向模式(n = 1),一个模式两个(n = 2),三(n = 3)模式。箭头指示方向的水粒子速度。实线和虚线表示界面位移的一半时间间隔。上层为斜压情况下没有显示速度,可以推断出从对称。

图5示意图显示前三个水平界面湖面波动模式:横向模式(n = 1),一个模式两个(n = 2),三(n = 3)模式。箭头指示方向的水粒子速度。实线和虚线表示界面位移的一半时间间隔。上层为斜压情况下没有显示速度,可以推断出从对称。

方程波传播方向相反,给出了方程的水平模式一(H1)驻波模式(图5(一个))

y (x, t) = cos (kx +) + cos (kx -) = 2 acos kx cos

组件波振幅= dy / 2或来描述/ 2根据接口考虑,角频率=科钦,k = 2 n / X是波长和波数和l T = 2 p / a波的周期。对于一个封闭的盆地,有1/2波长的H1假潮在一个湖泊,给予l = 2 l和一段时间的

T n甲n = 1为H1假潮是节点的数量分或半波长在水平方向上。

layer-averaged水平速度与H1湖面波动是最大的盆地的中心和给出的

这些垂直速度为零的边界,是纯粹的垂直运动(图5)。同样的表面假潮的mid-lake泥沙速度

振荡振荡电流低谷和准恒定。从各种各样的观察湖泊和水库显示表面和内部假潮

04:45

05:27 06:10 07:35

04:45

21:40 00:29 03:19

21:40 00:29 03:19

05:27 06:10 07:35

上午9点

纵向当前的速度ulong (cm / s)

图6 Near-bed速度概要文件一个小湖显示振荡性质和无滑动边界与湖面波动电流有关。观察超过一半的假潮时期在倍表示。概要文件偏移量都是策划和给定的速度范围。从Lorke Umlauf L,乔纳斯T,吴(2002)在低速湍流动力学振荡底部边界层分层盆地。环境流体力学2:291 - 313。

电流的典型范围0.02 - -0.20 m s - 1,最大~ 0.2 ms-1在风暴和接近零的无滑动沉积边界流由于摩擦(图6)。

高水平模式湖面(n > 1)也观察到在湖泊。这些所描述的线性波动方程的通解,初始条件的一致的倾斜界面,由所有更高水平的叠加模式。一般的解决方案是n = 1 v /

n = 1的水平模式一(H1)假潮,n = 2水平mode-two (H2)假潮,n = 3的水平mode-three (H3)假潮(图5)。无限的模式是可行的,每个都有减少振幅和能量随着模态数量的增加。基本的解决方案(即由只奇怪的模式。q (x, t) = 0时,n是偶数)直观地预计,因为只有奇怪的常微分方程有mid-basin位置的节点是零位移与初始均匀初始倾斜(图2和3)。通过计算相关的猿与每个模式,它可以表明,超过98%的波的能量H1中包含的模式,但之间的能量分布模式可能会影响共振迫使和盆地形状。

表面和内部的例子假潮时期各种水平模式表1中给出。潜力和动能形式之间的能量会通过波随时间周期性震荡(图2)。在t = 0, (1/2) 71 T1, T1(3/2)等潜在的波能量是纯粹的形式,在t = (1/4) T1 (3/4) T1 (5/4) T1,等纯粹是动能,导致湖盆内横向电流(图6)。对于非耗散系统,模态能量分布代表动能和势能的总和,是独立的时间。耗散过程将导致减少波振幅,但不是时期,随着时间的推移(表1);除非有足够的混合的thermo-cline导致分层的改变,因此有限公司连续表面湖面衰变振幅与每个时期的范围可以从3%(日内瓦湖)32%(伊利湖)。

垂直模式当密度垂直结构可能与三个或三个以上近似液层(图1 c, d),除了垂直模式一,横向模式一(V1H1)湖面(图2 b),更高的垂直模式支持湖面;例如V2H1等等。(图2)。三层系统有限公司

u 2 h, g = (1 - pjp2) hlh2 +(1 -π/ p3) hlh3 + (1 - M p2) h2h3和= h1 h2 h3 (1 - Pl = p2) (1 - p2和p3):

替换成的方程波的周期Tn = 2 l /区域给出了垂直mode-two的时期

表1中观察到表面和内部假潮时期从不同的湖泊和相关的振幅衰减

湖和位置T (h) T2 (h) T3, T4 (h) T5 (h) (h)分数下降幅度与每个连续的时期

表面湖面坦噶尼喀(非洲)1尼斯赚(苏格兰)山中(日本)1、2加尔达(意大利)1 ' 2

日内瓦(Switzerland-France) 1、2韦特恩湖(瑞典)1、2贝加尔湖(俄罗斯)1密歇根(Canada-USA) 1伊利(Canada-USA) 1 ' 2内部湖面Baldegg(瑞士)3卢加诺(Switzerland-Italy) 4温德米尔湖(英格兰)3苏黎世(瑞士)5尼斯湖(苏格兰)3日内瓦(Switzerland-France) 3

0.075	0.038	0.028
0.24	0.14	0.10
0.26	0.18	0.09
0.72	0.48	0.37
1.2	0.59
3.0	1.6	1.3
4.6
9.1	5.2	3.7
14.3	9.0	5.9
9.3	4.6	3.1
24	12	8.0
24	13	9
45	24	17
57	27	18
74年	46	0.099 4.2 - 0.322 14日11 22日18 威尔逊1 W(1972)湖面。在ChowVT (ed)。的进步Hydroscience 8: 1 - 94。 2吴AJ和农民DM(2003)湖面。麦格劳-希尔科技百科全书,9日版。纽约:麦格劳-希尔。 3雷明U和莫蒂默CH(1986)的测试扩展内部湖面Defant过程测定表面的湖面波动特征的湖泊。湖沼学和海洋学31:1207 - 1231。 4 hutter K, Salvade G,施瓦布DJ(1983)在北部盆地内部波动态卢加诺湖。地球物理和天体物理流体动力学27日:299 - 336。 5角W,莫蒂默CH和施瓦布DJ(1986)风致内部观察到苏黎世湖的湖面和建模。湖沼学和海洋学31:1232 - 1254。 波,横模态结构被定义为n。 垂直mode-two湖面时可以生成一个不对称的倾斜上下分层的接口层(昼夜和季节斜温层或斜温层的上、下边界)。实验室和现场数据表明,这类不对称有限压缩和扩张的介绍了斜温层顺风与逆风沿岸发生,分别在上升流的条件下(例如,图3 (d))。垂直模式的强度两个回应是假设的相对价值取决于Wedderburn和湖数字。V2响应发生小W和大型LN(强大的上层界面的倾斜,大型剪切在表层的基础和一个相对安静的低界面);而V1响应发生小棒大LN(可比倾斜的接口和强大的速度在深水层)。 更高的垂直模式盆地规模内波曾被观察到在几个湖泊,一般突然风脉冲后兴奋的一个初始V1H1响应,然后演变成V2湖面波动(如木湖,上神秘的湖,湖康士坦茨湖)。共振佳人迫使(例如,Alpnach湖),倾斜的盆地地形和不平等的密度分层的层之间的差异会导致更高的垂直的优惠激励模式。 内部模式在一个连续的分层 的两层的假设分层在湖泊很多是不合适的吗浅水湖泊(H < ~ 15米;例如,Frains湖)和hypolom-nion很深的湖泊(例如,贝加尔湖)或者分层具有显著的化学(生理盐水)组件(例如,莫诺湖)。这些系统更好的建模使用连续分层的倾斜等密度线由于风设置捕获LN。在风应力的松弛,连续分层将支持一系列的垂直盆地规模模式。每个模式是由相关的频率 这是依赖于盆地几何和可用于计算波的周期T = 2 p / o。每个垂直模式的结构m波函数所描述的是厘米,这是获得从线性长波方程常数N 厘米(z) =罪(jp z), m = 1, 2, 3,是衡量内部地层的波浪诱导垂直位移在特定深度。例如,V1波最大内部位移在中深,而V2波在1/4H容积和负位移3/4H(图7);显示的地层特征。 波函数不包含知识的实际波振幅,因此往往是规范化的Cm - 1 < < 1。厘米的效用是它可能从Taylor-Goldstein方程数值计算任意N (z)配置文件,因此确定波模式,支持一个特定的水体分层。盆地规模的纵向模态结构,单一模式或模式的组合,不得计算当波振幅已知- q (z, t)«厘米(z) (t)。纵向模态结构可以预测整个盆地在时间和空间上通过假设一个波形■q (x, z, t)«厘米(z) v (x, t);这通常是一个湖面或sech2余弦函数孤波(稍后介绍)。 水平速度剖面波动引发的尺度与波函数的梯度codCm / dz(图7 (b))。速度场的解析表达式,可以发现在分层流文本。连续速度概要文件在图7中符合深度平均电流提出了如图2所示。在这两种模型,尽管技术上不正确的(图6),free-slip底部边界已经假定。相应的速度从这些模型并不代表流底部边界附近。

继续阅读:退化湖泊盆地范围内波

这篇文章有用吗?

+ 1 0