I0
-
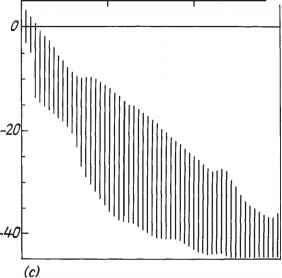
- 图4.1(持续)。
在开始讨论之前所学的理论模型系统我们注意到外部参数上面列出的决心,反过来,大气之间的相互作用过程的PBL和自由的氛围,和海洋PBL和深海之间。但是因为各种物质的涡动通量降低,因为他们远离两个环境的接口和人外周血的外边界消失,然后边界层之间的交互,实现自由大气和海洋深处而不是艾迪转移,相反,通过流程不同的起源。有序垂直运动和湍流的渗透到邻近的non-turbulent域(夹带)作为连接链接系统的大气PBL-free大气、海洋和海洋PBL-deep。它还应该记住,承担培养系统中的速度场的弛豫时间远小于在自由的气氛,尤其是在深海。因此,当检查两人外周血隔离从海洋大气系统动力学和随后的分析不考虑反馈的机制与自由大气和海洋深处发现在许多情况下是合理的。人讨论已知的自治系统的大气和海洋行星边界层的这些条件。
4.1.1理论模型利用先验信息的大小和概要文件涡流粘度系数
在分析观测数据在风和冰漂移的“弗拉姆号”漂移,南森注意到冰漂流在中央北极倾斜的右边30 - 40°的风向。由地球自转和他解释说这一事实表明,因为上层海洋层驱动运动由冰电流引起的海洋中应偏离风向甚至超过30 - 40°。理论研究这个问题是由埃克曼(1902),结果符合南森的定性结论。埃克曼(1905)提出了一个理论确认顺时针旋转(在北半球)的漂移当前的速度深度和举出一些论点支持使用获得的结果来描述风速随高度变化。这个想法后来被Akerblom意识到独立(1908)和《报告》(1912)。建议住在长度上报告》的工作,因为他是第一个把行星边界层海洋和大气的一个动态系统。
在静止的条件下平行和等距等压线PBL的运动是由以下方程描述:
~ kMi ^ + f (vt - Vgi) = 0;~公里p - f (Ui (Usi) = 0, (4.1.1)
z z d: dz: d: dz,呃vt是风速的组件或漂流;子是面向垂直坐标的海洋大气中的垂直向上和向下(原点位于自由海洋表面);下标我就值1、2 = 1符合大气PBL, i = 2符合海洋PBL;所有其他名称都是一样的。
方程(以下4.4.1)假设速度分量Vg2, Ug2的地转流等于零,公里的涡粘性系数在每个PBL与高度和固定保持不变,并满足以下条件在海气界面和相当大的距离:
ui = vi v2 = > ^ miPI j - = ~ kM1p2 - - >
dp, dv2公里\π-¡= ~ kuiPi 7 - 2 Zj = 0, dz1时
U;= > U h Vi = > Vi Zj = >有限公司(4.4.3)
已知的边界条件(10/24/11),意思是连续性的速度和动量通量在海洋表面的自由;的有界性条件(4.4.3)描述速度足够大的高度范围内的各自的培养。
最后一个表达式的风和气流速度的垂直廓线形式
Ui = Ugi + e ~ aiZil(情况- Ugi)因为atzt + (v0 - Fgi)罪;z;), j vt = Vgi + e ~::, ((v0 - Vgi)因为,z;-(情况- Ugi)罪,zj, j情况,v0在海洋表面流速组件定义的平等
利用现有涡粘性系数的估计当时Koschmider(1938)计算风速的变化的大气和海洋中漂流的速度。原来系统中的速度分布两人外周血被翻倍埃克曼螺旋和空气的流速界面不是零,同时与地转风方向(见图4.2)。从这个,特别是遵循结论风的逆时针旋转速度矢量与第二高度大气层。
进一步发展的理论是通过Shvets(1939)和Hesselberg (1954)。获得更好的计算结果和实验数据之间的协议考虑大气压力梯度随高度的变化。这样做,Hesselberg Shvets不同,分配滑移条件作为空气界面的边界条件。两位作者认为涡粘性系数是独立的高度,和预先指定的。计算风速随高度的变化被发现是定性接近观察变化:风速的快速增长是明显在第一个几百米,然后在500年和1000米下降甚至完全终止,并再次开始在更大的高度速度增加。
报告》的推广模型的情况下,海洋表面覆盖着自由漂浮的冰被Laikhtman提出(1958)。在这种情况下,空气动量通量的连续性条件界面取代了预算方程力在一个单位
这篇文章有用吗?

