德国气象局全球气象模型GME中无线电掩星数据的同化
D.平格尔和A.罗丁
德国气象局三维变分数据同化系统中GPS无线电掩星的同化需要GPS无线电掩星弯曲角前向算符。为了优化前向算子的设置,对不同的一维和三维弯曲角度前向算子进行了评估。来自CHAMP、GRACE-A和FORMOSAT-3/COSMIC卫星的无线电掩星数据的创新统计数据与基于同化方案中指定的背景和观测误差的估计数据进行了比较。本文进行了一个数值实验来评估同化射电掩星数据对天气预报分数的影响,并与仅同化常规观测数据的实验进行了比较。
1 DWD的数据同化
在数值天气预报程序的同化步骤中,在预报本身运行之前,使用观测信息更新气象模式的状态。气象观测的常规来源是现场数据,如无线电探空仪、地面站测量数据、飞机数据和浮标。此外还有卫星遥感测量,例如某一波长在最低点处的辐射。
全球定位系统无线电掩星(GPS RO)数据是一个相对较新的和有价值的观测信息来源,它将额外的温度和湿度信息引入模型(Healy et al., 2007b;Wickert et al., 2009)。反渗透数据的优点是具有良好的垂直分辨率,不受多云条件的影响(多云条件通常影响亮度测量,cf. McNally(2002)),缺乏基本偏差和几乎均匀的全球覆盖。
在德国气象局(Deutscher Wetterdienst, DWD),观测数据(包括GPS无线电掩星数据)的同化将由
Deutscher Wetterdienst (DWD),奥芬巴赫,德国(电子邮件保护)
三维变分(3D-Var)同化法。同化是以统计上最优的方式进行的,考虑到先前分析的观测值y、预测值xb(模型背景)以及模型和观测值的误差特征,由它们各自的误差协方差矩阵B和r给出。因此,彻底规范观测和预测误差在数据同化中具有高度相关性。在同化过程中,代价函数J包含控制变量x(网格模型场)的偏差惩罚项,其中控制变量x(网格模型场)来自背景xb,而观察值y来自它们的模型等值H(x),在另一侧被最小化:
J (x) = Jb +乔= 2 (x - xb) TB-1 (x - xb) + 1 (y - H (x)) TR-1 [y - H (x)]。(1)
前向算子H将模型背景数据映射到观测空间。对于现场测量,H只是对观测位置进行插值。在遥感测量中,H更为复杂,通常是非线性的。分析x由代价函数J相对于控制变量x的梯度的零给出,
dJ = B-1 [x - xb] + HtR-1 [y - H(x)] (2)
dx,其中H是H的雅可比矩阵。切线算子和伴随算子分别计算H与右边和左边向量的乘积。分析增量为x - xb = [HtR-1H + B-1]- 1htr -1[y - H(xb)] = BHt[HBHt + R]-1[y - H(xb)]。
方程(3)的解在观测空间(Physical-space Statistical Assimilation System, PSAS)中进行。这意味着与模型空间中的最小化相比,要求解的数值方程的大小显著减小。用x - xb = BHTz (4)
和解决
对于观测空间中的z。采用外部牛顿算法和内部预条件共轭梯度(CG)算法相结合的方法,在迭代过程中求解非线性问题。非线性通过迭代Eq. (5), H在当前估计x;处线性化,表示为H;(Daley和Barker, 2000):
随后,根据式(4)将解z与预测误差协方差进行后乘,确定模型状态变量的分析增量。
基本上,相位延迟、弯曲角度或折射场可以起到被同化观测的作用。在DWD中,选择弯曲角度作为观测值,因为它们可以可靠地说明显著的背景和观测误差,并且可以在不考虑水平均匀性或各向同性的情况下推导出来。因此,要实现一个合适的前向算子H,将观测位置的模型背景映射到相应的第一猜测弯曲角度。
2弯曲角度前向算子的评价
在无线电掩星同化的准备工作中,一个重要的步骤是为前向算符找到一个合理的设置,该设置适合在特定的操作应用条件下进行数据同化。以创新的标准差(观测值和初猜测值的差异)作为基准准则,对一维和三维弯曲角度前向算子进行了评价。三维射线追踪算子的标准差最小,优化后的一维正向算子与三维正向算子的性能接近。
评估一种可能的弯曲角正向算子设置,提供弯曲角a(p)作为冲击高度p的函数的背景剖面,是RO观测同化的先决条件。考虑了三维射线追踪模型和一维模型作为前向算子:
射线追踪算子H3d (Gorbunov and Kornblueh, 2003)被认为是最适合物理现实的,因为它考虑了温度和湿度大气场的沿射线和横射线水平梯度,以及掩星过程中射线切向点的漂移。射线跟踪算子的一个缺点是对计算资源(时间和内存)的要求很高。
一维正演算子是基于球对称大气场的假设。它应用了阿贝尔逆变换
折射剖面
(其中c1 = 77.6 K hPa 1和c2 = 3.73■105 K2 hPa 1)由温度T、压力p和水汽分压pv以上的水平单点,即掩星点xoc推导出来。通过将水平扩展的占用事件简化为单点xoc,忽略了切向点漂移。此外,xoc的选择给正演模型带来了一定的不确定性。为了至少在一定程度上模拟切线点的漂移,为了测试目的,已经实现了三个版本的一维正向算子,每个版本都考虑了不同的确定的xoc:第一个版本H1d在xoc处执行反Abel变换,如相应的弯曲角度观测数据集中所给出的那样。对于第二个版本H1dmn, xoc被确定为掩星剖面最低20 km处的单个射线切线点的平均值(在首字母缩写“1dmn”中附加缩写“mn”表示)。第三个版本H2d分别对掩星剖面的每条射线应用Abel逆变换,xoc是射线的切线点。与之前的两个版本相比,这种方法有望最好地模拟切向点漂移。
测试不同正向算子性能的数据集是波茨坦geoforschungsen -trum (GFZ) 2005年1月和7月提供的CHAMP(挑战性小卫星载荷)和GRACE-A(重力和气候恢复实验)相位延迟数据集,使用规范变换CT2方法处理到DWD的弯曲角度(Gorbunov和Lauritsen, raybet雷竞技最新2002,2004a,b;Gorbunov et al., 2006)。DWD全球气象模型GME (Majewski et al., 2002)三小时预报场作为模型背景。创新的统计性质,即观察和最初猜测的差异,然后考虑作为评价不同正向算子的标准。
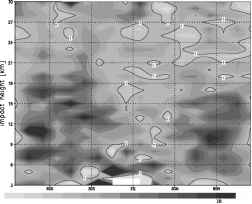
图1a-c显示了2005年1月一维正向算子H1d、H1dmn和H2d三个版本的(O - B)标准差与三维射线追踪算子H3d各自值的比值的纬向平均值(bin大小为1 kmx10°)。对于所有三个一维正向算子,对于大多数区域和高度,比值的值大于单位值(考虑全局均值时,它们严格大于单位值)。这表明射线追踪前向算子在标准偏差方面表现最好。
在比较不同一维正向算子时,接受CT2给出的掩星点的算子H1d表现最差(图1a)。相应的标准偏差超过H3d各自的值,最多可达8%。然而,与其他热带地区相比,热带地区的比例要小得多。这与以下事实有关:由于大气动力学的差异,温度和湿度的水平梯度在热带地区不如在外热带地区明显。由于提供这些梯度是运算符H3d与H1d相比的特征之一,因此在热带地区,一维和三维运算符的弯曲角度值趋于可比性。
与算子H1d相比,算子H1dmn在~8 km以上冲击高度的标准差有所降低(图1b)。这表明平均过程使xoc更接近对流层上部和平流层下部射线的切线点。
版本H2d的第一个猜测值,对每条射线应用Abel逆变换,与预期的射线追踪结果最接近(图1c)。
图1弯曲角度前向算子的评价:一维前向算子标准差之比(a) H1d (top),
(c) H2d(下)相对于射线追踪前向算子H3d, 2005年1月
-
- 0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1。(
st.dev。200501 . 1 dmn/3d
st.dev。200501 . 1 dmn/3d
-

- 0'98 099 1 1'01 102 103 I' fh 1 05 1 06 1 07
st.dev。2 d / 3 d 200501
st.dev。2 d / 3 d 200501
-
- 只有1、3
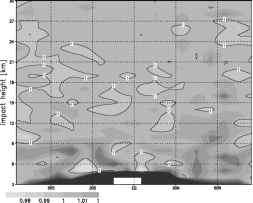
在冲击高度约10公里以上的大部分地区,与操作员H3d的差异小于1%。此外,与H1d和H1dmn相比,H2d的标准差比更为均匀。
但是,对于最低的射线,特别是在热带,更精细的版本H2d比更简单的版本H1d和H1dmn表现更差。这种效应可能与大多数掩星事件中,最低射线的切点位置偏离由较高射线的切点所描述的或多或少的直线有关。作为地理参考点的位置,这些“扭结”可能是不合适的选择。不过,有必要对这种影响进行彻底的调查。
在冲击高度km以下,射线追踪正向算子H3d在标准差方面明显更好。这可能是因为在这个高度以下,弯曲角度信号主要包含湿度信息(特别是在热带地区)。与温度相反,水蒸气是一个在水平尺度上与掩星程度相当的显著波动的量。这些波动是由算子H3d考虑的,而不是由一维正向算子考虑的。
图2显示了与图1c相同的数量,但为2005年7月。对流层低层标准差比值的极大值向北移动是很明显的,这与北半球夏季这些区域湿度的增加是相对应的。
弯曲角度前向算子的评价结果以另一种方式得到证实:为了更清楚地揭示算子性能的差异(以标准差表示),我们考虑了那些观测值(y)的创新统计量,其各自的第一猜测弯曲角度st.dev。2 d / 3 d 200507
st.dev。2 d / 3 d 200507

0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08
图2与图1c相同,但适用于夏季月份
0.98 0.99 1 1.01 1.02 1.03 1.04 1.05 1.06 1.07 1.08
图2与图1c相同,但对于夏季月份的数值(H(xb));至少相差光线追踪第一猜测值(Hsd(Xb))的一个给定分数;
|(高频(Xb));——(H3d (Xb));| > e■(H3d(Xb))i (9)
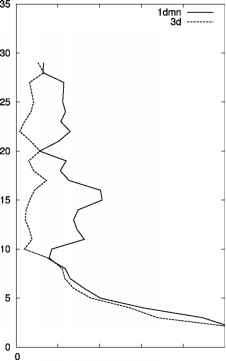
式中,F e {1d, 1dmn, 2d}表示一维正向算子的版本,H的分量用(H)表示;由式(9)选择的每个观测值(y)对应于用不同版本的一维正向算子和三维算子计算的背景值。为了测量观测值与背景值的接近度,我们确定了观测值y与背景值H1d(xb), H1dmn(xb), H2d(xb), H3d(xb)的每种不同组合的创新(y - H(xb))统计量。图3显示了用算子H1dmn和H3d选择的数据集的标准差(第一猜测值的百分比,全球平均值,2005年7月),e = 5%。H3d的标准差明显小于H1dmn的对应值,即用H3d得到的第一猜测值往往比用H1dmn得到的更接近观测值。与其他前向算子组合和不同e值的对应计算清楚地表明了性能
图3弯曲角度正向算子的评价:根据Eq.(9)所选观测值的H1dml]和H3d的标准差(e = 5%)
0.25
0.25
按Hu ^ H^mn ^ Hzd ^ Hid的顺序增加的弯曲角度前向算子的标准差。
虽然在创新统计水平上存在显著差异,但在冲击高度大于8 km时,优化后的一维正向算子与射线追踪结果的总体偏差很小(1-2%)。由于GPS反渗透观测的统计权重在此高度以下较小(由于湿度梯度导致的观测误差较大),这表明使用适当优化的一维弯曲角度前向算子进行操作同化,这与其他研究的结果一致(Poli 2006;Healy等人,2007a)。
在接下来的监测和同化实验中,采用优化的一维正演算子H1dmn代替射线追踪算子。
3监测
安排了对射电掩星观测的长期监测。为此,每月确定观测值和背景值差异的统计参数(O - B)。一般来说,观测到的弯曲角度与背景等效值一致,其偏差对应于同化系统中对背景和观测误差所作的假设。
弯曲角观测数据与对应的背景等效数据进行了比较,这些背景等效数据是通过应用一维逆阿贝尔变换前向算子(版本H1dmn,见第2节)从GME的预测场中获得的。GFZ的CHAMP和GRACE-A的近实时(NRT)弯曲角数据集和CDAAC/UCAR (COSMIC数据分析和存档中心/)的FORMOSAT-3/COSMIC(气象、电离层和气候星座观测系统)的数据集raybet雷竞技最新大学大气研究公司)。此外,GFZ对CHAMP和GRACE-A的近实时相位延迟数据集应用CT2方法(在DWD处)生成第三个数据集。CT2方法可以估计弯曲角观测误差的值,这些值不包括在GFZ的近实时弯曲角数据集中。因此,获得了关于掩星数据的附加统计信息。
一个质量控制应用于要监测的GPS RO数据:应用3a (O - B)检查来去除异常值。相对观测误差大于5%(相对于观测到的弯曲角度值)的观测结果被丢弃,这就删除了大部分热带对流层低层(湿度波动的影响)和平流层(残留的平流层波动引起额外的噪声)的观测结果。此外,弯曲角度的值被限制在区间[0,0.02]内,以排除由于管道工艺造成的误差。这些质量控制参数也应用于同化实验(见第4节)。
相应差异的统计特性,创新,被考虑到评估模型和观测弯曲角度值的一致性和相应的误差估计,并在接下来的段落中讨论。
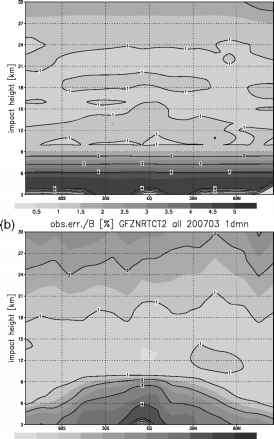
图4a-c显示了经过质量控制后可获得的反渗透剖面(料仓尺寸为1 km x 10°)的全球分布。CHAMP/GRACE-A和COSMIC轨道几何形状的不同导致了各自图中的不同模式。
图5、6、7、8和9显示了2007年3月三个数据集(O - B)创新的统计参数的纬向平均值(仓大小为1 km x 10°),下面将进行讨论。
由于CHAMP和GRACE-A近实时数据尚未包括对观测误差的估计,因此假设该数据集的观测误差与撞击高度之间存在简单的部分线性函数依赖关系(Healy和Thepaut, 2006)(见图5a):相对观测误差在0千米到10千米的撞击高度范围内从10-1%线性下降。在10km以上,假设观测误差为弯曲角度值的1%,直到达到6 × 10 - 6弧度的绝对下限。这种观测误差模型与CT2方法(图5b)和COSMIC方法(图5c)对CHAMP和GRACE-A的纬向变化观测误差形成对比。
平流层观测误差主要是由于电离层波动造成的。对于COSMIC和CT2推导的CHAMP/GRACE-A弯曲角度数据集,观测误差由几何光学推导的弯曲角度和气候学推导的弯曲角度之间的差异估计。对于掩星剖面的对流层部分,多径区域的信号跟踪(将由无线电全息方法解决)主导观测误差。对于COSMIC数据,观测误差是通过将多余相位信号中的涨落直接传播到弯曲角度而得到的。CT2方法利用变换后的信号波场运行谱的谱宽进行估计。关于观测误差估计方法的细节,见Gorbunov (2002);Gorbunov等人(2006)(CHAMP/GRACE-A with CT2)和CDAAC/TACC (2007a,b) (FORMOSAT-3/COSMIC)及其参考文献。
热带湿度对观测误差的影响与低纬度地区较高的相对观测误差值一致。在20 km撞击高度以上,CT2与COSMIC对CHAMP和GRACE-A的观测误差差异显著。这是由于使用了不同的气候学来估计误差的平流层成分。对比GFZ获得的近实时弯折角与CT2在DWD上获得的弯折角,可以明显看出CT2在10-20 km冲击高度上比GFZ保留了更多的掩星数据(参见图4a,b),但观测误差相对较大,尤其是在对流层的低层和高层(见图5b)。观测误差的高值导致在这些高度水平上丢弃了更多的观测值,如图4b所示。对于所有数据集,估计的观测误差(图5a-c)通常小于模式背景误差(图6,不同RO数据集的模式背景误差相同),特别是在额外热带的对流层上部。弯曲角度的背景误差Bb由3D-Var中指定的温度和相对湿度的背景误差协方差bf通过线性化观测算子计算得到:
图4 (a) CHAMP/GRACE-A (GFZ弯曲角),(b) CHAMP/GRACE-A (GFZ相位延迟,DWD CT2弯曲角),(c) COSMIC (CDAAC/UCAR弯曲角)的GPS RO剖面数量(仓尺寸为1 km x 1Ö0)
图4 (a) CHAMP/GRACE-A (GFZ弯曲角),(b) CHAMP/GRACE-A (GFZ相位延迟,DWD CT2弯曲角),(c) COSMIC (CDAAC/UCAR弯曲角)的GPS RO剖面数量(仓尺寸为1 km x 1Ö0)
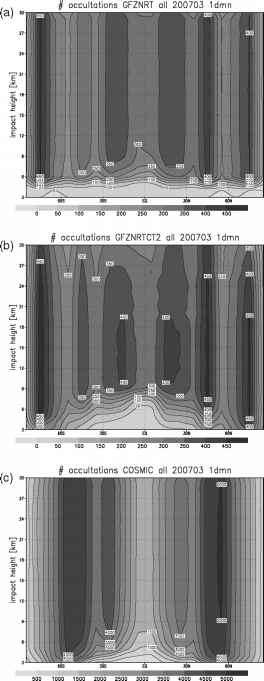
图5 (a) CHAMP/GRACE-A(函数法,GFZ弯曲角),(b) CHAMP/GRACE-A (GFZ相位延迟,DWD CT2弯曲角),(c) COSMIC (CDAAC/UCAR弯曲角)的弯曲角观测误差估计
图5 (a) CHAMP/GRACE-A(函数法,GFZ弯曲角),(b) CHAMP/GRACE-A (GFZ相位延迟,DWD CT2弯曲角),(c) COSMIC (CDAAC/UCAR弯曲角)的弯曲角观测误差估计
-
![bg.error/B [%] GFZNRT all 200703 1dmn](//m.zandimusic.com/radio-occultation/images/3396_6_80.jpg)
- bg。error/B [%] GFZNRT all 200703 1dmn .输出说明
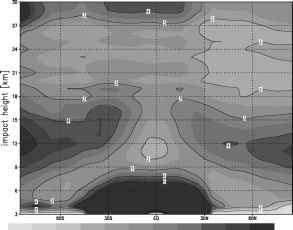
图6 GME模型中估计的弯曲角度背景误差(由t和rh处的背景误差协方差通过切线线性算子ffidmn得到的第一猜测值的百分比)
图6 GME模型中估计的弯曲角度背景误差(由t和rh处的背景误差协方差通过切线线性算子ffidmn得到的第一猜测值的百分比)
在大气变化较大的热带急流区,弯折角的背景误差分布较大。另一个极大值位于热带对流层下部。在这里,湿度变化对弯曲角度背景误差的贡献最大,可达15%。COSMIC和CT2算法估计的观测误差(图5)也显示了热带地区的最大值。如果不进行质量控制,这些观测误差会大得多,并且会达到与背景误差相似的值。在低热带地区,只有相对较少的观测值通过标准(参见图4),因此观测误差与背景误差相同或更小,这是在同化中使用观测值的先决条件。
图7a-c显示了三个数据集的创新的标准差a。由于湿度的影响更明显,热带地区的标准偏差值通常更高。在撞击高度~18 km处的最大标准差可能是由重力波的存在引起的。超过25公里的偏差是由于电离层波动造成的,考虑到L1和L2相位的差异,只能部分纠正这种波动。从气候学反演的弯曲角度剩余的较大差异通常通过拟合来抑制。如果用阿贝尔反演从弯曲角度得到温度分布,那么在较高海拔合理的弯曲角度值是很重要的。如果将前向算子应用于大气剖面,以导出反演弯曲角度的对应模型,那么只要反演误差被正确指定,它们就不是必需的。这是由CT2检索算法完成的。在这种情况下,模型背景将用于
图7 (a) CHAMP/GRACE-A (GFZ的弯曲角度),(B) CHAMP/GRACE-A (GFZ的相位延迟,CT2在DWD的弯曲角度),(c) COSMIC (UCAR/CDAAC的弯曲角度)的创新(O - B)/B(第一猜测值的百分比,H1dmn弯曲角度前向算子)的标准差
st.dev。(0-B)/B [%] GFZNRT all 200703 1dmn st.dev。(0-B)/B [%] GFZNRT all 200703 1dmn

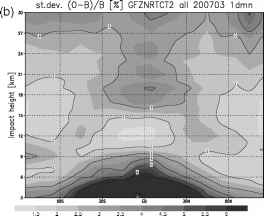
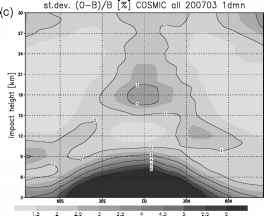
图8 (a) CHAMP/GRACE-A (GFZ弯曲角),(B) CHAMP/GRACE-A (GFZ相位延迟,DWD CT2弯曲角),(c) COSMIC (UCAR/CDAAC弯曲角)的创新标准偏差(O - B)与估计标准偏差的比值
D.平戈尔和a .罗丁(a) st.dev.(0-B)/est.err。[%] GFZNRT all 200703 1dmn
D.平戈尔和a .罗丁(a) st.dev.(0-B)/est.err。[%] GFZNRT all 200703 1dmn
图8 (a) CHAMP/GRACE-A (GFZ弯曲角),(B) CHAMP/GRACE-A (GFZ相位延迟,DWD CT2弯曲角),(c) COSMIC (UCAR/CDAAC弯曲角)的创新标准偏差(O - B)与估计标准偏差的比值
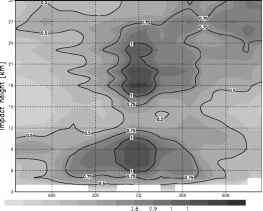
(b) (0 b) / est.err st.dev。[%] GFZNRTCT2 all 200703 1dmn
(b) (0 b) / est.err st.dev。[%] GFZNRTCT2 all 200703 1dmn
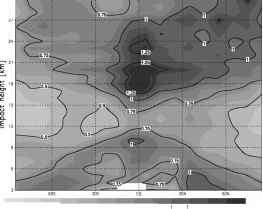
(c) st.dev。(O-B) / est.err。[%]宇宙所有200703 1dmn
(c) st.dev。(O-B) / est.err。[%]宇宙所有200703 1dmn
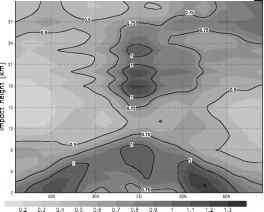
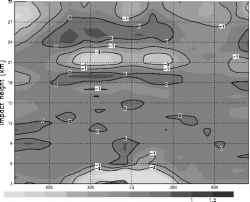
图9 (a) CHAMP/GRACE-A (GFZ的弯曲角度),(B) CHAMP/GRACE-A (GFZ的相位延迟,CT2在DWD的弯曲角度),(c) COSMIC (UCAR/CDAAC的弯曲角度)的创新偏差(O - B)/B(第一猜测值的百分比,ff1dmn弯曲角度前向算子)
-
- 0.5 0 0.5
偏差(0-B)/B [%] GFZNRTCT2所有200703 1dmn偏差(0-B)/B [%] GFZNRTCT2所有200703 1dmn
-
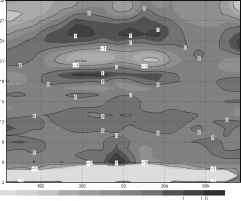
- 0.5 0 0.5
偏差(0-B)/B [%] COSMIC all 200703 1dmn偏差(0-B)/B [%] COSMIC all 200703 1dmn
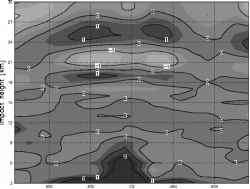
变分同化方案中的正则化。创新的标准差与其估计值进行比较,观测误差与背景误差的二次和eest = (e2bs + ebg)1/2。图8a-c显示了标准偏差与估计偏差a/eesi的比值。总的来说,CHAMP和GRACE-A观测到的弯曲角度与相应的背景等效角度相当吻合,并且在同化系统中对背景和观测误差所作的假设范围内。对于大多数区域和高度水平,比值小于统一,表明观测值和背景值的一致性比从误差规范中估计的更好。在热带对流层上部,相对较高的比值a/eest再次表明存在背景误差模型中没有考虑到的重力波。
如图9a-c所示,创新的偏差相当小,但在上部表现出显著的垂直振荡模式对流层和平流层在热带和中纬度地区,这可能与GME背景模式的性质有关。此外,CT2处理的CHAMP和GRACE-A数据(图9b)的总体偏差似乎比GFZ和COSMIC相应的NRT结果略负(图9a,c)。
4同化实验
在同化实验中测试了同化装置,包括优化后的弯曲角度前向算子。无线电掩星观测对天气预报质量的影响是通过吸收六颗FORMOSAT-3/COSMIC卫星的RO数据和常规数据的实验来评估的。在南半球观测到对预报分数的积极影响。
为了估计反渗透观测数据的最大影响,并对同化系统进行必要的优化,进行了首次反渗透同化实验。同化实验是在同化时间窗口为3小时的DWD 3D-Var上进行的。同化的观测数据是来自6颗FORMOSAT-3/COSMIC卫星的RO弯曲角度数据和常规现场数据。在相应的对照实验中,常规数据是唯一的观测来源。
图10a显示了南半球500 hPa的地球势,实验分析与IFS分析(ECMWF)差异的标准偏差显著降低。对于北半球,所分析的场的平均变化为中性(未显示)。
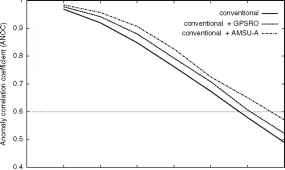
后续的预测运行是为了评估对预测结果的影响。大气场的异常相关系数(ANOC)可以量化预报质量,衡量预报偏差与模式气候学吻合分析的偏差之间的相关性。图10b为南半球500 hPa的地球势场异常相关系数,为对照实验,实验
500hPa地势对IFS分析控制SH GPS RO SH的偏差
500hPa地势对IFS分析控制SH GPS RO SH的偏差
05/10 05/12 05/14 05/16 05/18 05/20 05/22 05/24 05/26 05/28 05/30 06/01 00:00 00:00 00:00 00:00 00:00 00:00 00:00 00:00 00:00 00:00 00:00 00:00
ANOC地球势500 hPa SH 2007051400至2007053100(18次预报)
05/10 05/12 05/14 05/16 05/18 05/20 05/22 05/24 05/26 05/28 05/30 06/01 00:00 00:00 00:00 00:00 00:00 00:00 00:00 00:00 00:00 00:00 00:00 00:00
ANOC地球势500 hPa SH 2007051400至2007053100(18次预报)
72 96
预测时间(h)
图10南半球实验GPS RO观测数据同化:(a) 500hpa处地势分析差值与IFS的标准差,(b)异常相关(ANOC)系数
72 96
预测时间(h)
图10南半球实验GPS RO观测数据同化:(a) 500hpa处地势分析差值与IFS的标准差,(b)异常相关(ANOC)系数
此外,还包括RO观测,以及同化常规观测和AMSU-A数据的实验(使用18个预测)。RO同化导致南半球ANOC显著增加,温度场也有类似的结果。值得注意的是,在吸收AMSU-A辐射观测资料和常规数据时,由于RO导致的预测分数的改善已经是预期改善的一半。在北半球,地球势和温度仍然可见ANOC的轻微退化,其原因仍有待确定。
温度和湿度与无线电测深和飞机数据的相应测量值的验证表明,南半球反渗透观测同化实验的标准偏差显著降低(未显示)。
5的结论
评价了三种不同版本的一维和三维光线跟踪弯曲角度前向算子在三维变分数据同化系统中的性能。射线跟踪算子考虑了水平梯度和射线的切向点漂移。一维算符的不同版本都应用了逆阿贝尔变换,假设大气场是球对称的,但都反映了不同程度的切向点漂移。考虑撞击高度为8 km以上的掩星观测数据的初猜测差值的标准差,三维正演算子与优化后的一维正演算子相差不超过2%。因此,选择一个适当优化的,数值上更便宜的一维前向算子用于操作数据同化系统似乎是合理的。来自CHAMP、GRACE-A和FORMOSAT-3/COSMIC的近实时无线电掩星弯曲角度数据集的监测已经进行了几个月。观测-先猜想差异的标准差完全在同化系统的误差界估计之内。同化弯曲角度观测的实验表明,与仅同化常规数据的对照实验相比,南半球的预报质量有了显著提高,证明无线电掩星数据是一个有价值的气象信息来源。
感谢波茨坦地球观测中心(GFZ)可靠地提供了CHAMP和GRACE-A数据集的无线电掩星数据,包括离线和近实时处理。感谢FORMOSAT-3/COSMIC计划免费提供无线电掩星数据。我们感谢Michael Gorbunov为我们提供CT2处理方法和弯曲角度前向操作符。德国教育和研究部支持了与GEOTECHNOLOGIEN研究计划中近实时提供和使用无线电掩星数据有关的研究项目NRT-RO。
参考文献
CDAAC/TACC (2007a)大气数据反演(ROAM):在中性大气中反演无线电掩星信号的算法。http://cosmic-io.cosmic.ucar.edu/cdaac/doc/文档/ roam05.doc,http://tacc.cwb.gov.tw/cdaac/doc/documents/roam05.docCDAAC/TACC (2007b)电离层数据反演(GMRION):反演电离层无线电掩星信号的算法。http://cosmic-io.cosmic.ucar.edu/cdaac/doc/文档/ gmrion.pdf,http://tacc.cwb.gov.tw/cdaac/doc/documents/gmrion.pdfDaley R, Barker E (2000) NAVDAS源书2000:NRL大气变分数据
同化系统。技术代表,海军研究实验室,蒙特雷,加拿大Gorbunov ME(2002)电离层校正和无线电掩星数据的统计优化。
高晓峰,王晓峰,李晓峰(2003)GNSS无线电掩星数据的变分同化原理。报告350,马普气象研究所,联邦大街55号,D-20146汉堡
高布诺夫ME, Lauritsen KB(2002)无线电掩星数据的规范变换方法。哥本哈根丹麦气象研究所科学报告02-10,可在http://www.dmi.dk/dmi / sr02 - 10. - pdf
傅立叶积分算子分析波场及其在射电掩星中的应用。高晓峰,王晓峰,王晓峰等(2004b)无线电掩星数据的正则变换方法。见:Kirchengast G, Foelsche U, Steiner AK (eds)掩星探测大气和气候,施普林格,柏林海德堡,pp 61-68 Gorbunov ME, raybet雷竞技最新Lauritsen KB, Rhodin A, Tomassini M, Kornblueh L(2006)无线电全息滤波,误差估计和无线电掩星数据的质量控制。刘志强,王志强(2006)利雷竞技csgo用CHAMP GPS无线电掩星测量的同化实验。地球物理学报,61 (1),doi: 10.6038 / cjg20160604。王晓明,王晓明,王晓明,等(2007a)基于二维弯曲角观测的GPS无线电掩星数据同化。中国气象学报(英文版
王晓明,王晓明,王晓明,王晓明,等(2007b) GRACE-A和CHAMP GPS无线电掩星弯曲角剖面的联合预测。大气科学通报8(2):43-50
Majewski D, Liermann D, Prohl P, Ritter B, Buchhold M, Hanisch T, Paul G, Wergen W(2002)可操作的全局二十面体-六方格点模型GME:描述和高分辨率测试。McNally AP(2002)关于气象敏感地区云的发生及其对先进红外测深仪的影响的说明。中国气象学报,28 (4):381 - 381,doi: 10.3969 / j.i ssn . 1008 - 102.2008.05.021
Poli P(2006)水平梯度对GPS无线电掩星观测算子的影响。II:快速大气折射率梯度算子(FARGO)。Wickert J, Michalak G, Schmidt T, Beyerle G, Cheng C, Healy SB, Heise S, Huang CY, Jakowski N, Köhler W, Mayer C, Offilier D, Ozawa E, Pavelyev A, Rothacher M, Tapley B, Viehweg C (2009) GPS无线电掩星:CHAMP, GRACE和FORMOSAT-3/COSMIC的结果。地球大气与海洋科学20(1):35-50,doi:10.3319/TAO.2007.12.26.01(F3C)
继续阅读:GPSRO功能
这篇文章有用吗?



![bg.error/B [%] GFZNRT all 200703 1dmn](http://m.zandimusic.com/radio-occultation/images/3396_6_80.jpg)


