饱和或onephase流
当一个非混相流体,如潮湿的空气和水,充满孔隙空间,流是相对饱和阶段。除非通过非常粗糙的雪,如大粒度的深度灰白色,流动缓慢,足以用达西定律描述。在这种情况下,流体的流速vk结合压力和引力成正比。因此,
重力梯度力压力
这里,K是饱和或内在的渗透率,x是一个空间坐标沿着流动方向,^之间的角方向和垂直向下流动,g是重力加速度,和pk、nk、和pk是压力,动态粘度和密度的液体K (t =空气=水)。因为雪是很少被水浸透的(除了当水池塘上方冰层或冻土),方程(2.19)主要用于空气流动模型。
饱和空气渗透率饱和或内在渗透孔隙结构的特性,决定了缓解和传输速率雪液体。K通常是衡量迫使空气通过一个雪样本测量流量和压降(Chacho和约翰逊,1987;艾伯特et al ., 2000)。因此常常被称为“空气”渗透。透气性雪广泛变化类型和变化随着时间的推移变质作用的结果。在寒冷的网站体验很少或没有条件或风漂流,融化雪的渗透率通常随着时间的增加其质地变粗。低于前几米在积雪中,然而,渗透率降低的压力导致上覆层压实和水晶烧结(Albert et al ., 2000)。在季节性雪,表面的渗层张成的空间一天内可以经历戏剧性的变化因此日晒和表面加热(Albert阶石,2000)。
图2.12(在约旦等等。1999 b)编制的测量Kfrom几个调查人员和比较其与冰的分数(1 - 0)测量范围在两个数量级从3 x的真空度对细粒度的m - 2, wind-packed雪(低孔隙度和小孔径)600 x的真空度m - 2为大粒度的深度灰白色(中等孔隙度和非常大的孔隙大小)。虚线表示雪渗透率为不同类别的一般范围观察到贝德等等。(1939)。大多数测量属于外边界的分类方案。Sturm报道的(1991)和约旦et al。(1999 b)深度霍尔在阿拉斯加和加拿大北部尤其是高和最有可能反映出非常大的毛孔和可能存在的垂直间隙孔(Arons Colbeck, 1995)。艾伯特和阶石(2000)还表明,冰在季节性积雪层渗透,虽然他们的透气性大大低于周围的雪。
散点图2.12表明,孔隙度的本身并不是一个有用的指标K .如果孔隙结构理想化作为管的包,K变得成正比管或孔隙直径的平方以及孔隙度(Dullien, 1992)。其他因素,如孔隙形状、孔互连,粒度分布,和弯曲度也影响k .管式模型适用于土壤和密集的雪花,小雪是不现实的,当颗粒形状和特定区域主导因素。因为孔隙大小很难直接测量,这是通常从孔隙度的组合(或估计雪密度)和颗粒直径。通过装箱渗透率测量分为equi-density组,清水(1970)
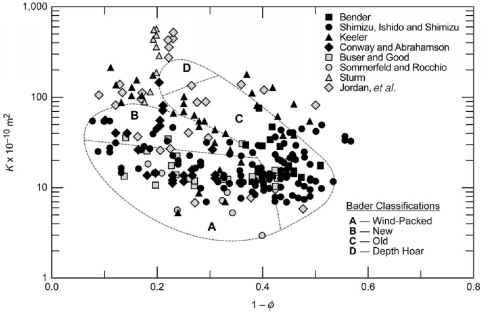
图2.12。测量渗透率K和冰分数(1 - 0)基于实验室的观察本德(1957),石田和清水(1958),清水(1960年),齐勒(1969 b),清水(1970),康威和亚伯拉罕森(1984),布塞尔和良好(1986),索姆费尔德和Rocchio (1989), Sturm(1991),和约旦et al . (1999 b)。虚线表示巴德et al。(1939)分类方案(在约旦et al ., 1999 b,版权1999;版权约翰威利& Sons有限。复制许可)。
图2.12。测量渗透率K和冰分数(1 - 0)基于实验室的观察本德(1957),石田和清水(1958),清水(1960年),齐勒(1969 b),清水(1970),康威和亚伯拉罕森(1984),布塞尔和良好(1986),索姆费尔德和Rocchio (1989), Sturm(1991),和约旦et al . (1999 b)。虚线表示巴德et al。(1939)分类方案(在约旦et al ., 1999 b,版权1999;版权约翰威利& Sons有限。复制许可)。
解耦与密度和粒度的关系,推导出广泛使用公式:
K = 0.077 0078 ps d2 e-0 = 0.077 e - 7 - 153 a - ^ d2。(2.20)
有趣的是,他的经验函数从理论上正确的单位长度的平方。如果我们正常化K d2,见图2.13(乔丹et al ., 1999 b),由此产生的关系显示明显降低K与冰分数。而清水细粒度的数据集是有限的,wind-packed雪,图2.13中的趋势表明,他的函数也适用于其他雪类型。最近的测量卢西亚诺和艾伯特(2002),然而,发现他的公式产生渗透估计不同观测一个数量级以上。
图2.13还显示了理论曲线组合的光盘和领域。对于一个给定的孔隙和颗粒半径,床组成的薄圆盘的长宽比25有大约8倍的特定区域组成
1000年
”问
0.01
0.001
0.0001
0.00001
*清水函数
阿哈迪•索姆费尔德和Rocchio O和艾伯特乔丹et al。
阿哈迪•索姆费尔德和Rocchio O和艾伯特乔丹et al。

图2.13。降低渗透率K d 2与冰分数(1 - 0)在实验室观察的基础上石田和清水(1958),清水(1960),清水(1970),索姆费尔德和Rocchio(1989),哈代和艾伯特(1993),和约旦et al . (1999 b)。行显示减少清水函数(Eq。2.20)和理论解决方案(乔丹et al ., 1999 b)床上的薄盘(a =直径,b =厚度、a / b = 25)和球体。光盘和球体半径相等(在约旦et al ., 1999 b,版权1999;版权约翰威利& Sons有限。复制许可)。
的领域,因此对流体产生更高的阻力。这表明,除了谷物半径和孔隙度,-通常更高的新雪的表面体积比是一个重要的参数描述雪渗透率。
的自然分层积雪通常导致更耐流比水平方向在垂直(石田和清水,1958;Dullien, 1992)。卢西亚诺和艾伯特(2002)报告测量渗透率的各向异性或方向性降雪和积雪实地测量,并得出结论,层间渗透率差异占变异大于定向的差异在一个层。因为垂直分层媒体计算系列电阻中,渗透率是由最耐药或低渗透地层。
被迫在多孔介质和空气自然对流的空气运动可以产生两种机制:(1)压力差异,迫使流(windpumping或强制对流)或(2)产生浮力的温度梯度热对流(也称为自然
表2.4每米温差为自然对流的发生。
表2.4每米温差为自然对流的发生。
雪类型 |
x的真空度平方米 |
Wm-1K-1 |
常数通量ATcrit |
常数T ATcrit |
|
深度灰白色 |
200年 |
200年 |
0.05 |
10 |
15 |
新雪 |
80年 |
200年 |
0.10 |
50 |
77年 |
One hundred. |
300年 |
0.20 |
80年 |
123年 |
|
积雪 |
40 |
300年 |
0.20 |
200年 |
308年 |
Wind-pack |
10 |
300年 |
0.20 |
800年 |
1234年 |
对流)。在有些情形下,被迫和自然对流的空气可以发生在自然雪。
当温暖的衬底之间存在很大的温度梯度和冷的表面,空气密度变化和导致浮力空气循环在多孔介质;这被称为自然对流。权力et al。(1985)详细的理论在雪自然对流。无因次瑞利数控制对流的发生及其强度,并给出了
在方程(2.21),p0a参考空气密度,英国《金融时报》的热膨胀系数,在驱动温差,HS是雪的深度,A = W (PaCp,)。
发病的临界瑞利数Racrit自然对流是大约27当表面渗透在恒定的温度和底部边界与恒温不透水。当底部边界与恒热流不透水,临界瑞利数大约是18岁。共同价值观的渗透和导热系数的各种雪类型,表2.4列出了所需的温差会自然对流的发生在1米深的积雪下两个底部边界条件。因为每米50°C的自然温度梯度非常罕见,这是极不可能的自然对流发生在自然雪除了包由深度的情况下没有干预层灰白色。Sturm和约翰逊(1992)是测量温度的多孔,薄的亚北极积雪(主要由大深度灰白色晶体组成)支持的存在自然对流。
强制对流在雪是由自然压力变化引起的。它已经表明,湍流风在一个平面上,等压面压力变化,和经过表面凹凸的风都能造成压力扰动垂直传播到雪(Colbeck, 1989;克拉克和沃丁顿,1991)。气压的变化可能会导致慢,在雪近地表低速空气流动。风湍流导致高频压力波动传播毫米或厘米到雪。“拖”压力差异,引起的气流在表面粗糙度(如跨雪脊),可能导致更强大和更持续的气流深处雪。
雪会影响分层通风通过地层的渗透率的差异。艾伯特(1996)表明,即使在假设雪在给定层是各向同性,各层之间的差异影响地下空气流场。例如,埋效果(如霍尔)层可以作为渠道增加横向流穿过积雪。
空气的强制对流在雪雪能影响其他进程,如升华(艾伯特,2002),化学变化(沃丁顿等等。,1996;麦康奈尔et al ., 1998;艾伯特et al ., 2002),或传热(艾伯特与哈代,1995;约旦,et al ., 2003;安德烈亚斯,et al ., 2004)。
继续阅读:不饱和或两相的流
这篇文章有用吗?