热力学简论

2.1概述

我们主要研究对象的大气是由可压缩气体构成的。压缩性对这些大气中温度的垂直分布有深远的影响。随着事情的进展，垂直温度的变化反过来会强烈地影响地球的气候，这一点将变得越来越清楚。raybet雷竞技最新为了处理这些影响，有必要了解一些热力学知识——尽管只是一点点。本章并不打算成为热力学的完整课程。它只能提供处理行星气候基本问题所需的关键热力学概念和公式的摘要。raybet雷竞技最新假定学生已经获得(或将获得)热力学一般主题的更基本的理解在其他地方。

2.2一些观察

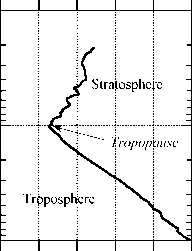
图2.1中在地球热带地区测量的温度剖面介绍了研究一般行星大气所感兴趣的大部分特征。它是通过释放一个仪器气球(无线电探空仪)而获得的，气球从地面向上漂浮，并在上升时发回温度和压力的数据。压力随高度而单调下降，因此压力越低代表海拔越高。图中使用的压力单位为毫巴(mb)。一巴几乎是地球上海平面的平均压力，一巴有1000毫巴。

压力是一个很自然的垂直坐标。许多测量大气剖面的设备直接报告压力而不是高度，因为前者通常更容易测量。更重要的是，气候物理学中的大多数问题只需要了解温度和其他量随压力的变化;raybet雷竞技最新在相对较少的情况下，需要知道与给定压力对应的实际高度。压力也很重要，因为它是决定组成大气的气体状态的基本热力学变量之一。大气在本质上向我们展示了一个方便地展开高度的热力学图。在整个过程中，我们将使用压力(或其对数)作为我们的基本垂坐标。

1000

1993年3月15日，12Z 2.00 S 169.02 W

150 180 210 240 270 300温度(开尔文)

1993年3月15日，12Z 2.00 S 169.02 W

1000

海拔高度(公里)

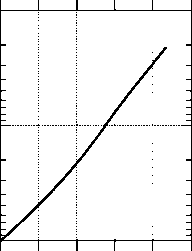
图2.1:左面板:在热带太平洋某一点测量的温度分布图。右图:对应的海拔高度。这些测量数据是由1993年3月15日在12Z(格林威治标准时间的缩写)发射的无线电探空仪(“气象气球”)获得的。

然而，由于各种原因，人们可能仍然想知道给定的压力水平在什么高度。通过对气球的高度跟踪，或使用第2.3节中描述的方法，可以以压力的形式获得测量高度。图2.1右侧面板显示了图2.1所示测深高度与压力的关系。我们可以看到高度和压强的对数近似成线性关系。这就是为什么在对数图上绘制量与压力的关系是很方便的。如果po代表了最大的兴趣压力，那么- ln(p/po)是一个很好的高度坐标，因为它是正的，并且随着高度的增加而增加。

现在我们可以回到对温度分布的关键方面的讨论。测温最显著的特点是温度随海拔高度而下降。这是一个熟悉的现象，谁经历过天气在高山，但探测结果显示，气温下降的高度比任何山峰的采样高度都要高得多。这是在太平洋上空拍摄的，所以它也表明温度下降与山脉表面的存在无关。温度下降一直持续到一个被称为对流层顶的临界高度，在这个高度以上(100mb，或在这个测深中为16公里)开始随着高度1而增加。下面的部分大气对流层顶是它被称为对流层，而其上方的部分是平流层。“Tropo”来自希腊语词根“翻转”(如“翻身”)，而“Strato..”指分层。使用这个术语的原因很快就会清楚。同温层是由法国仪器气球飞行的先驱Leon Phillipe Teisserenc de Bort在1900年发现的。

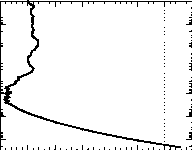
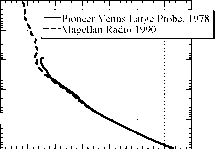
我们所展示的声音是典型的。事实上，在许多其他行星的大气中也遇到了类似的模式，如图2.2中金星、火星、木星和土卫六的大气所示。与地球的情况一样，这些大气的较低部分显示出急剧减少温度随高度变化，这让位于一个在更高海拔地区温度更平缓下降，甚至上升的区域。以金星为例，令人惊讶的是，用两种完全不同的技术进行的测量，在一天的不同时间探测大气的不同位置，并且相隔十年，但在测量的重叠区域却非常一致。这既证明了测量技术的准确性，也证明了金星上缺乏我们通常所说的“天气”，至少就温度变化所反映的情况而言是这样。以火星为例，温度下降在夏天的下午表现得最明显，当时火星表面仍然受到太阳的温暖。随着夜晚的临近，上层气温下降仍然明显，但低层大气迅速冷却，导致低层逆温，或温度升高的区域。在火星的极地冬季，整个大气明显冷却，而且比其他情况下的等温温度要高得多。

从山地天气的经验来看，地球大气层的温度随高度而下降是早就知道的。在温度计发明后不久，它就成为了定量研究的目标，并且很早就被认为是对那些寻求理解大气的人的挑战。这是登山家和科学家霍勒斯·本尼迪克特·德·索绪尔(Horace Benedict de Saussure, 1740-1799)的主要工作之一。在寻找解释的过程中，人们采取了许多错误的步骤，甚至连傅立叶这样的伟人也在正确答案揭晓之前采取了错误的步骤。正如本章剩余部分所示，基于热力学和垂直混合的一些简单想法至少提供了解释温度下降的核心

1虽然地球大气垂直剖面的最低温度是不同层之间转换的最明显指标，但我们最终将能够提供一个基于更动态的对流层顶定义。在我们最终确定的定义中，对流层顶不需要用最低温度来标记，尽管在地球上，最低温度仅略高于动态定义的对流层顶，因此可以作为对流层顶位置的一个近似指标。

高度。在第三章的末尾，我们将介绍一个理论对流层顶高度这抓住了问题的本质;对流层顶高度的理论将在第4章、第5章和第6章的各个点上日益复杂地重新讨论。尽管如此，在理解温度随高度下降的速率和对流层顶高度的地理分布方面仍然存在一些严重的差距。在第三章和第四章中，我们将看到行星的能量收支受到温度垂直结构的关键影响;因此，彻底理解这一特征对于任何行星气候理论都是至关重要的。raybet雷竞技最新

2.3理想气体的干热力学2.3.1理想气体的状态方程

我们主要关注的三个热力学变量是:温度(用T表示)、压力(用p表示)和密度(用p表示)。温度与组成气体的分子中每个分子的平均动能成正比。我们总是以开尔文为单位来测量温度，这和摄氏度是一样的，只是偏移量使绝对零度——即分子停止运动的温度——在0开尔文时达到。在摄氏温度下，绝对零度出现在-273.15摄氏度左右。压力定义为单位面积上与气体接触的表面所受的力，方向垂直于表面2。它与表面的方向无关，可以在给定的位置通过使表面越来越小来定义。在我们在本书中使用的mks单位中，压力以帕斯卡(Pa)测量;1帕斯卡是1牛顿每平方米的力，或相当于1千克/(ms2)。由于历史原因，大气压力通常用“巴”或“毫巴”来测量。1巴，或相当于1000毫巴(mb)，大约是地球当前大气的平均海平面压力。我们经常会误用mb作为压力单位，因为这个单位对大气科学家来说听起来很舒服。 For calculations, though, it is important to convert millibars to Pascals. This is easy, because 1 mb = 100 Pa. Hence, we should all learn to say "Hectopascal" in place of "millibar." It may take some time. When pressures are quoted in millibars or bars, one must make sure to convert them to Pascals before using the values in any thermodynamic calculations.

密度就是单位体积内所含气体的质量。以mks为单位，计量单位为kg/m3。

对于完美气体，这三个热力学变量由完美气体状态方程联系起来，可以写成p = knT (2.1)

其中p是压强，n是单位体积的分子数(与密度成正比)，T是温度。k是玻尔兹曼热力学常数，一个具有单位温度能量维度的通用常数。它的值只取决于测量热力学量的单位。N是气体的粒子数密度。为了将n与质量密度联系起来，我们将n乘以单个气体分子的质量。几乎所有的质量都来自分子中的质子和中子，因为相比之下，电子的重量几乎为零。而且，一个中子的质量和一个原子的质量差别很小

2压力可以等效地定义为单位时间内每单位面积通过气体中放置的一个小箍向两个方向传递的动量量。这个定义等价于施加力的定义，因为当一个速度为v，质量为m的分子从一个表面弹性反弹时，动量变化为2mv，但在任何给定的时间内，只有一半的分子向表面移动。动量通量的定义，相反，计数分子通过环的两个方向

木星

木星

100 150 200 250 300 350 400 450吨

金星

金星

100 200 300 400 500 600 700 800吨

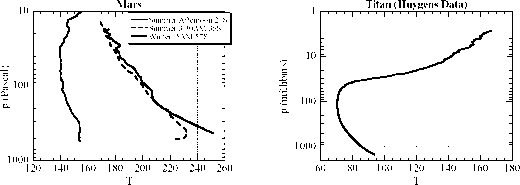
图2.2:木星部分大气(左上)、金星部分大气(右上)、火星部分大气(左下)和土卫六部分大气(右下)的垂直温度廓线。金星麦哲伦号和火星的数据分别来自麦哲伦号(1980年代末)和全球勘测者号轨道飞行器对大气中无线电传输的观测。关于金星大气较低部分的信息来自于1978年4个先驱者金星探测器中的一个(其他探测器显示了类似的模式)。木星的数据来自伽利略探测器的减速测量。完整的火星剖面数据集揭示了相当大的季节和地理变化。这里显示的剖面是由火星全球勘测者在南半球拍摄的。最温暖的一次出现在1998年夏季亚热带地区的下午晚些时候，而在其他条件相似的情况下，第二温暖的一次出现在夜间。图中显示的最冷的火星探测信号来自冬季的南极地区。100帕斯卡= 1 mb

图2.2:木星部分大气(左上)、金星部分大气(右上)、火星部分大气(左下)和土卫六部分大气(右下)的垂直温度廓线。金星麦哲伦号和火星的数据分别来自麦哲伦号(1980年代末)和全球勘测者号轨道飞行器对大气中无线电传输的观测。关于金星大气较低部分的信息来自于1978年4个先驱者金星探测器中的一个(其他探测器显示了类似的模式)。木星的数据来自伽利略探测器的减速测量。完整的火星剖面数据集揭示了相当大的季节和地理变化。这里显示的剖面是由火星全球勘测者在南半球拍摄的。最温暖的一次出现在1998年夏季亚热带地区的下午晚些时候，而在其他条件相似的情况下，第二温暖的一次出现在夜间。图中显示的最冷的火星探测信号来自冬季的南极地区。100帕斯卡= 1 mb质子，所以对于我们的目的，分子的质量可以取为M•y，其中y是质子的质量，M是分子量-给出分子中中子和质子数的整数。(元素的单个原子的等效计数是原子量)。 The density is thus p = n • M • y). If we define the Universal Gas Constant as R* = k/y the perfect gas equation of state can be rewritten

P = m pt (2.2)

以mks为单位，R* = 8314.5(m/s)2K-1我们还可以定义一个气体常数R = R*/ m。例如，干燥的地球空气的平均分子量为28.97，所以Rdryair = 287 (m/s)2K-1，以mks为单位。

如果y的单位是千克，那么1/y就是构成一千克所需的质子数。这个大数字被称为摩尔，通常被用作分子数量的测量单位，就像人们通常以打为单位数鸡蛋一样。对于任何一种物质，其质量(公斤)等于该物质的分子量的数量将包含一摩尔的分子。例如，2千克的H2是1摩尔的氢分子，而32千克最常见的O2是1摩尔的氧分子。如果n的单位是摩尔/立方米，而不是每立方米分子数，那么密度将是p = n•m。我们还可以定义克摩尔(或简称摩尔)，它是生成一克所需的质子数;这个数字被称为阿伏伽德罗数，大约是6.022•1023。

一般来说，当一种气体足够稀薄，以至于构成气体的分子之间的力所储存的能量可以忽略不计时，它就遵守完美气体定律。偏离完美气体定律对于金星的稠密大气是很重要的，但对于电流的目的地球大气层无论是在火星，还是在木星或金星大气层的上层，完美气体定律都可以被视为热力学的精确模型。

完美气体概念的一个引申是分压定律。这就是说，在一定体积的气体混合物中，每一种气体的行为都与单独占据该体积时一样。由一种气体产生的压力称为该气体的分压。假设一种气体是物质a(相对分子质量Ma)和物质B(相对分子质量MB)的混合物。这两种气体的分压是

或者说,

其中Ra = R*/Ma, RB = R*/MB。两个方程中出现的温度是相同的，因为热力学平衡规定了系统中所有组分的温度都是相同的。气体中任意两种组分的分压之比是描述气体组成的一种方便的方法。由式2.3可知，pa/pb =«A/nB，因此A的分压与B的分压之比也就是A的分子数与B的分子数之比，这个比值称为摩尔混合比。当我们提到一个不加限定的混合比时，我们通常指的是摩尔混合比。另外，也可以用一种组分的分压与气体总压之比来描述组分(在双组分例子中为pa/(pa + pB))。将Eq. 2.3中的两个分压方程相加，我们看到这也是A的分子数与总分子数的比值;因此，我们将用摩尔浓度来表示这个比例3。如果£a是a与B的摩尔混合比，则

“体积混合比”或“浓度”常与“摩尔”交替使用，如“ppmv”表示“摩尔”。百万分之一体积。”这个术语的原因是气体的体积被给定的数量在一个固定的温度和压力成正比,气体的分子数包含摩尔浓度是£/(1 +£),从我们看到的摩尔浓度和摩尔混合比几乎相同的物质非常稀释(例如^ 1)。我们将使用符号nA在书中表示物质的摩尔浓度。

计算摩尔浓度为nA = nA/(nA + nB)和= nB/(nA + nB)的混合气体表现为平均分子量为M = nAMA + nBMB的完美气体。(即导出总压力pA + pB与总密度pA + pB的关系式，并确定有效气体常数)。计算地球干燥空气的平均分子量。(按分子数计算，干地空气主要由78.084%的N2、20.947%的O2和0.934%的Ar组成。)

质量混合比是给定气体中A物质的质量与B物质的质量之比，即pa/pb。由公式2.4可知，它与pa ma pa的摩尔混合比有关

Pb Mb

在本书中，我们将使用符号r表示质量混合比，n表示摩尔混合比，并在必要时添加下标以区分所涉及的物种。另一种测量成分的方法是比浓度，定义为给定物质的质量与包裹总质量的比值(例如，在双组分情况下pa/(pa + pB))。我们将使用符号q(必要时加上下标)来表示某种物质的具体浓度。利用分压定律，混合物中A物质的比浓度与摩尔浓度(pa pa ma)有关。

ptt M ptt M

其中M为混合物的平均分子量，其平均值根据物种的摩尔浓度加权计算，如练习2.3.1所示。

我们刚才定义的所有比率都很方便使用，因为与密度不同，只要所考虑的成分不发生凝结、化学反应或其他形式的内部源或汇，它们在空气膨胀或收缩时保持不变。因此，对于可压缩气体，如果两种组分a和B之间的混合比与位置无关，那么它们之间的相对混合是很好的。

相对于混合所需的特征时间而言，如果成分的产生或破坏速度很慢(如果有的话)，那么它们就会在大气层深处充分混合。在地球大气层中，氧气和氮气的混合比例在地表以上约80公里处几乎是恒定的。二氧化碳在空气中的混合比例在地表源附近(如燃烧大量燃料的城市地区)或地下会有很大差异森林的树冠当光合作用活跃时。然而，在远离地表的地方，二氧化碳的混合比例变化不大。在相对缓慢的混合平流层中，可以检测到百万分之几的变化，这与工业时代化石燃料二氧化碳排放的上升趋势有关。还可以探测到与地表源的变化有关的对流层混合比的季节性和半球间的小波动。不过，在大多数情况下，我们可以认为二氧化碳在大气中混合得很好。相比之下，水蒸气在这个量上有很强的力量。为了看到这一点，写n = n /V，其中n是分子的数量，V是它们所占的体积。理想气体定律可以写成V = (kT/p)N的另一种形式。因此，标准体积之比等于摩尔混合比，以此类推。像“ppmv”这样的缩写表示摩尔混合比是常见和方便的，因为“v”可以明确地提醒我们，我们谈论的是体积(即摩尔)混合比或浓度，而在“ppmm”这样的缩写中，人们会想知道第二个“m”是指“质量”还是“摩尔”。

它是地球大气中的内部汇，因为它在那里是可凝结的;因此，它的混合比例在垂直和水平上都有相当大的变化。目前，二氧化碳、甲烷和氨在地球上是不可凝结的，但在较冷的行星大气中，它们的凝结作用会变得显著。

习题2.3.2 (a) 2000年，大气中二氧化碳的浓度约为370ppm。pco2fptot的比值是多少?估算海平面二氧化碳分压，单位mb。摩尔浓度与摩尔混合比是否有显著差异?空气中二氧化碳的质量混合比是多少?空气中碳(以二氧化碳的形式)的质量混合比是多少?也就是说，为了在1公斤空气中产生二氧化碳，需要燃烧多少公斤碳才能变成二氧化碳?注:空气的平均分子量约为29。(b)地球空气中O2的摩尔浓度约为20%。在海平面上，呼吸1升的空气含有多少克氧气(1000mb)?在珠穆朗玛峰(又名珠穆朗玛峰)的顶端。 "Mt. Everest," about 300mb)? Does the temperature of the air (within reasonable limits) affect your answer much?

2.3.2比热与能量守恒

能量守恒是热力学大厦所依赖的三大支柱之一。当用物质状态的变化来表示时，它被称为热力学第一定律。当气体膨胀或收缩时，它确实会随着边界的移动而对环境产生作用力。因为压强是每单位面积的力，功是力乘以距离，所以体积dV膨胀过程中所做的功就是pdV。这是必须添加到气体包裹中的能量，以使体积增加。对于大气，以单位质量为基础写热力学关系更方便。V除以体积中包含的质量得到p-1，其中单位质量的功是pdp-1。这并不是能源核算的终结。在保持体积不变的情况下，改变物质单位质量的温度会改变分子在各种运动中储存的能量cv dT，其中cv是一个比例因子，称为恒定体积下的比热。例如，在保持体积不变的情况下，将1kg空气的温度提高1K需要大约720焦耳的能量。 For ideal gases, the specific heat can depend on temperature, though the dependence is typically weak. For non-ideal gases, specific heat can depend on pressure as well.

20个学生和一个教授在一个20米乘20米乘3米的绝缘良好的教室里。教室里的每个人都以100瓦(1瓦= 1焦耳/秒)的速度释放能量。教室里一片漆黑，只有一台电脑和一台液晶投影仪(LCD)，它们的耗电量高达200瓦。教室内充满1000mb压力的空气(不另收费)。房间是密封的，因此没有空气可以进出，初始温度为290K。在一小时的讲座中，教室的温度会上升多少?

结合这两种对能量变化的贡献，我们得到了为了实现温度和体积的变化，每单位质量必须添加的能量量的表达式:

SQ = cv dT + pdp-1 (2.7)

利用完全气体定律，热平衡可以重新写成

SQ = cvdT + d(pp-1) - p-1dp = (cv + R)dT - p-1dp (2.8)

根据这个关系，我们可以确定恒定压力下的比热，cp = cv + R，这是使单位质量升温1K，同时使其膨胀到足以保持压力恒定所需的能量。

我们用来测量温度的单位是一种人工制品，是某个研究人员曾经决定放在对冷热有反应的设备上的标记。由于温度与物质的每个分子的能量成正比，将比例常数设置为单位并简单地使用能量作为温度的测量是有意义的。这不是常见的做法，人们有机会利用玻尔兹曼热力学常数k，它表示温度和能量之间的比例关系。更准确地说，温度为T的系统中每个自由度的平均能量为1kt。例如，由刚性球形原子组成的气体，每个原子有三个自由度(每个原子可以移动的方向一个)，因此每个原子的平均能量为|kT;一个可以以旋转或振动的形式储存能量的分子将有更多的自由度，因此在任何给定的温度下，每个分子都有更多的能量。能量-温度关系是由一个重要的热力学原理，即均分原理，它指出在平衡状态下，一个系统的每个自由度在系统总能量中所占的份额是相等的。与光速等物理常数相比，玻尔兹曼常数不应该被认为是宇宙的基本常数。它只是一个单位转换因子。

2.3.3熵、可逆性和位温;第二定律

我们不能使用Eqn 2.8来定义一个状态(p, T)相对于参考状态(po, to)的“热含量”Q，因为从一个状态到另一个状态所需的热量取决于在压力-温度空间中到达那里的路径;右边的eqn2.8不是一个精确的微分。但是，将方程除以T，利用完美气体定律，可以得到精确微分方程:

ds = 5-TQ = cpT - RJ = cPdln(Tp-R/Cp) (2.9)

假设cp是常数。这个方程定义了熵，s = cp ln(Tp-R/ cp)。熵是一个很好的量，因为它是一个状态变量——它在两个状态之间的变化与从一个状态到另一个状态的路径无关。影响一团物质的过程是绝热的，如果它发生时没有从这团物质中增加或损失热量。根据定义，绝热过程5Q = 0。因此，绝热过程保持熵不变，只要系统状态的变化足够慢，系统在任何时候都保持接近热力学平衡。后一个条件对于所有与我们有关的大气现象都是满足的，但也可能被违反，例如，在以前封闭的气体爆炸性绝热膨胀进入真空的情况下。对于比热取决于温度和压力的气体，对于不均匀气体混合物，以及对于非理想气体，熵也可以被定义。

热力学第二定律指出，能量封闭系统的熵永远不会减少，这种系统在演化过程中既不增加也不减少能量。从分子相互作用的微观性质正式推导出这一定律在许多方面都是一项未完成的科学工作，但是熵增加的趋势——即无序程度的增加——似乎是由大量相互作用的成分组成的系统的几乎普遍的特性。熵保持不变的过程是可逆的，因为它可以双向进行。

第二定律也许更直观，当以以下方式重述时:热量从从系统中较热的部分到系统中较冷的部分，导致系统朝着温度均匀的状态发展。为了证明这种说法与熵增加原理是等价的，考虑一个具有均匀压力的隔热气体盒，但在这个盒子里，质量的左半部分温度为Ti，质量的右半部分温度为T2 < Ti。现在假设我们将一定量的热量从盒子的左半部分传递到右半部分。这种转移使净能量不变，但它改变了熵。具体地说，根据式2.9，两部分气体的熵变之和为ds = (- i)£Q。由于T2 < Ti，只有当>为0时，这个变化才为正，它表示气体从较热的部分转移到较冷的部分。熵可以通过进一步的传热来增加，直到Ti = T2，此时达到最大熵态。

第二定律赋予宇宙以时间之箭。如果一个人观看一个封闭系统的电影，看到系统开始时温度波动很大(低熵)，然后发展到温度均匀的状态(高熵)，他就知道时间在向前流逝。如果人们看到一个热均匀的物体自发地产生了很大的温度不均匀，那么人们就知道电影是倒着播放的。注意，第二定律只适用于封闭系统。如果一个子组件与外界交换能量，并增加宇宙其他部分的熵，它的熵就会降低。这就是冰箱的工作原理。

熵是一个非常普遍的概念，我们只看到了它最基本的实例。对于接近热力学平衡的均匀理想气体，可逆过程(即等熵过程)和绝热过程的概念是等效的，但是当将这一概念扩展到包含混合气体的更复杂系统时，必须谨慎。例如，如果一盒温度为T的气体，左半部分是纯N2，右半部分是纯O2，那么当两种气体自发混合时，即使没有能量进入盒子，熵也会增加。熵仍然可以根据¿Q/T的变化来定义，但它需要仔细注意¿Q的确切含义以及热量变化应用于哪些子系统。本章“进一步阅读”部分所提供的参考资料，对熵在解决热力学问题中的应用提供了更深入和更普遍的理解。

现在让我们回到基本的问题上来。熵可以用来确定空气块在绝热压缩或膨胀时温度的变化。这很重要，因为它告诉我们，如果一小部分大气从低空(压力大)被抬升到高空(压力低)，温度会发生什么变化，前提是抬升速度非常快，空气团几乎没有时间与周围环境交换热量。如果初始温度和压力为(T, p)，那么熵守恒告诉我们，绝热压缩或膨胀到压力po时的温度为Tp-R/Cp = T0p0 R/Cp。这使我们定义潜在温度d = T (p) -R/Cp(2.10)。

它是一个空气包裹的温度，如果绝热降低到一个参考压力。和熵一样，绝热过程的位温也是守恒的。

为了理解图2.1测深中暖空气上方的冷空气为何没有立即发生不稳定，我们只需看看图2.3所示的相应位温分布。该图表明，势温随高度单调增加。这个剖面告诉我们，高空的空气是冷的，但如果它被推到较低的高度，压缩就会使它变暖到比地面温度高的程度

1993年3月15日12Z

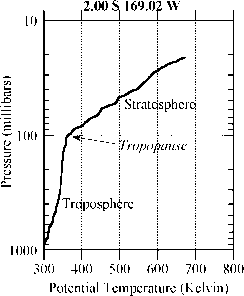
图2.3:图2.1测深的干势温度分布图

周围的空气，因此具有积极的浮力，将倾向于浮回原来的水平，而不是继续下降。我们也看到了平流层的名字来源:那里的潜在温度随着高度的增加而急剧增加，所以空气团对垂直位移非常有抵抗力。这一部分大气因此是高度分层的。

对流层是稳定的，但梯度为0，弱得多。在可压缩的大气中，搅拌良好的层将具有恒定的0而不是恒定的T，因为前者对于由快速垂直位移引起的绝热过程是守恒的。这就是对本质的解释为什么温度随高度而降低:湍流搅拌使对流层向常数0松弛，产生干绝热

T(p) = 0•(p) R/cp (2.11)

在这个公式中，0具有恒定值T(po)。

在干绝热层上，斜率dlnT/dlnp的值为R/cp。从公式2.9中的第一个等式可以看出，即使R/cp依赖于温度和压力，这个结果仍然有效。一般来说，斜率d ln T/d lnp提供了一个方便的测量温度在垂直方向上急剧下降的方法;正值对应温度随高度而降低，因为压力随高度而降低。那么干绝热斜率就是R/cp。在大气科学中，通常用- dt /dz(即递减率)来描述温度结构，但在很少的情况下，高度z是气候计算的方便坐标。raybet雷竞技最新除非另有说明，我们将(有点非常规地)使用术语递减率来表示斜率d ln T/d ln p干绝热递减率就是R/cp。(见问题??以探索该术语的更常规用法。)

从图2.3可以明显看出，有些东西阻止6完全混合。观察这一点的等效方法是将观测到的温度分布与干绝热进行比较。例如，如果图2.3中1000mb的温度为298K的空气被干式绝热提升到对流层顶，那里的压力为100mb，那么温度将为298.()2/7，即154.3K(使用地球空气的R/cp = 2/7的值)。这比观测到的188K要低得多。我们很快就会看到，在地球大气中，水蒸气的凝结是起作用的因素之一，尽管它不是影响对流层温度分布的唯一因素。是什么决定了对流层梯度，这个问题目前在很大程度上仍未解决，尤其是在热带地区以外。

空气的R/cp值接近两个小整数之比，这并非偶然。这是均分原则的结果。利用统计热力学的方法，可以得出由n个自由度的分子组成的气体R/cp = 2/(n + 2)。利用气体常数的比热表达式，绝热系数也可以写成R/cp = 1 - 1/y，其中7 = cp/cv;为了精确地相等，7 = 1 + 2/n。几种常见大气气体7的实测值见表2.1。氦接近于没有内部自由度的分子的理论值，这强调了在典型的行星温度下，电子运动的激发在热存储中起不到什么作用。当n = 5时，双原子分子的值最接近理论值，比增加两个旋转和一个振动内部自由度所期望的值少一个。在三原子分子中，水的作用大致上是n = 6，而二氧化碳的作用更接近于n = 7。甲烷和氨这两种最复杂的分子的特征也是n = 7。热力学无法获得分子的所有经典自由度，这是量子理论的结果。 Since the energy stored in states of motion of a molecule in fact comes in discrete-sized chunks, or "quanta," one can have a situation where a molecule hardly ever gets enough energy from a collision to excite even a single vibrational degree of freedom, for example, leading to the phenomenon of partial excitation or even non-excitation of certain classical degrees of freedom. This is one of many ways that the quantum theory, operating on exceedingly tiny spatial scales, exerts a crucial control over macroscopic properties of matter that can effect the very habitability of the Universe. Generally speaking, the higher the temperature gets, the more easy it is to excite internal degrees of freedom, leading to a decrease in 7. This quantum effect is the chief reason that specific heats vary somewhat with temperature.

练习2.3.4 (a)一架商用喷气式客机在300mb的高度巡航。外面的空气温度是240K。为了使乘客能够呼吸，周围的空气被压缩到机舱压力为1000mb。如果空气被绝热压缩，机舱温度会是多少?你认为航空公司如何处理这个问题?(b)讨论金星的温度图2.2所示的是干CO2绝热层的剖面。对夏季下午的火星探测做同样的事情。(c)假设木星探测是在干燥绝热层上进行的，估计大气的R/cp值。根据你的结果，木星大气的主要成分可能是什么?还有什么气体可能与主导气体混合?

2.4不均匀混合物的静稳定性

一个大气是静态不稳定的，如果一个空气团从它原来的位置移动，倾向于继续上升或下降，而不是回到它原来的位置。这种状态会自我混合，直到变得稳定。静态稳定对行星气候很重要，因为它会影响垂直混合，从而形成行星raybet雷竞技最新的对流层。

	水	甲烷	二氧化碳	N2	O2	H2	他	NH3
暴击。点T	647.1	190.44	304.2	126.2	154.54	33.2	5.1	405.5
暴击。点p	221. e5	45.96 e5	73.年代25e5	34.0 e5	50.43 e5	12.9 se5	2.2 se5	112.年代
三点T	273.15	90.67	216.54	63.14	54.3	13.95	2.17	195.4
三点p	611.	.117e5	5.1 s5e5	.1253e5	.0015e5	.072e5	.0507e5	.061e5
L vap (b.p)。	22.55 e5	5.1 e5	-	1.9 se5	2.13 e5	4.54 e5	.203e5	13.71 e5
L vap (t.p)。	24.93 e5	5.36 e5	3.97 e5	2.1 se5	2.42 e5	?？	?？	16.5 se5
L融合	3.34 e5	.5S6Se5	1.96 e5	.2573e5	.139e5	.5S2e5	?？	3.314 e5
L升华	2 s.4e5	5.95 e5	5.93 e5	2.437 e5	2.56 e5	?？	?？	19.年代9e5
p液体(b.p。)	95年s.4	450.2	1032.	S0S.6	1141.	70.97	124.96	6 s2。
p液体(t.p。)	999.S7	?？	雷竞技csgo1110.	?？	1307.	?？	?？	734.2
p固体	917.	509.3	1562.	1026.	1351.	党卫军。	200.	S22.6
cp (0 c / 1条)	1 s47。	2195.	S20。	1037.	916.	14230.	5196.	2060.
Y (cp /简历)	1.331	1.305	1.294	1.403	1.393	1.3 s4	1.664	1.309
表2.1:热力学性质			选择气体。		潜在的汽化热			给出了

在沸点(饱和蒸汽压达到1bar的点)和三重点。液体密度是在沸点和三点处给出的。对于二氧化碳，“沸点”是未定义的，所以液体密度是253K/20bar。请注意，最大值液态水密度为1000.00%/m3，在- 4℃时发生。固体密度在三点处或三点附近给出。所有的单位都是mks，所以压力被引用为Pa和适当的指数。因此，1bar在表中被写成1e5。

对于混合良好的大气，势温剖面说明了静态稳定性的全部情况，因为根据理想气体定律，当一个势温为00的空气块被提升到压力为pi < po的高度时，其密度将为p0 = p1/(R00•(p1/p0)R/Cp)。该区域的环境密度为pi = p1/(R01•(pi/po)R/Cp)。如果p0 > p1，位移的包裹将具有负浮力，并返回到其原始位置，当且仅当00 < 01，即当势温度随高度升高而升高．

对于不均匀的大气，这种情况就不再存在了，因为气体常数R取决于混合物的平均分子量，而平均分子量因地而异。作为一个例子，我们可以考虑一个大气，它具有统一的0，根据参考压力p0计算，但它由纯N2 (p > p0)和纯CO2 (p < p0)组成。有人立即注意到，系统在po处有一个不稳定的密度跳跃，因为密度在界面下方为po/RN2 0，在界面上方为po/Rco2 0。由于N2的分子量(28)比CO2的分子量(44)小，N2的气体常数比CO2的气体常数大得多。假设RN2 > RCO2，界面上方的密度大于界面下方的密度。这是一个不稳定的情况，N2层倾向于混合到CO2中，尽管恒定为0。

这种现象非常熟悉:这就是为什么氦气球在空气中上升，即使它们与周围环境的温度相同。氦的低分子量使得它比具有相同温度和压力的空气更轻(即密度更低)。

练习2.4.1理解下面这句话:“对于地球的大气层来说，潮湿的空气比干燥的空气轻。”如果一颗行星的大气主要是氢气，那么这种情况还会成立吗?

现在假设有一小部分氮气从界面下方上升到一个气压较低的高度p1。让包裹到达目的地时的密度为puft，环境二氧化碳的密度为pamb。密度差是

Pllft - pamb = ^ Rn2 (pi Jr^^ - Rco2 (p1/pal)-(R/cP)co2) (2.12)

这个方程中最大的影响来自于IN2 > ICO2这一事实，它确保N2在被提升时保持浮力。一个弱得多的影响来自于这样一个事实，即N2的I/cp(.286)略大于CO2(.230)。这调节了包裹被抬起时的密度差，但影响很小。即使抬升了很长的距离，使得pi/pa = .01，第一项中的压力因子也只是略大于第二项中的压力因子(3.74 vs. 2.89)，导致被抬升包裹的浮力略有降低。对于其他气体对，I/cp的差异可能更大，原则上它也可以朝相反的方向发展，增加而不是减少浮力。

对于组成和温度的任意剖面，人们可以定义一个势密度，这是一个空气包裹将具有的密度，如果压缩或绝热膨胀到一个标准参考压力po。利用气体定律和混合比守恒的事实(即在绝热压缩或膨胀时I/cp守恒)，势密度相对于参考水平po为

p(p|p0) = Ro

=IT (-)R/cp=p(p)(-)R/cp-i (213)

大埔RT

这个方程中的I和cp必须从压力p下的值中取，因为这些值是由成分决定的，在这个计算中，当包裹被移到参考压力po时，成分是固定的。当p(p|po)随p增加时，系统将是稳定的，即来自p < po的包裹在向下推至po时将具有正浮力，从而趋于返回其原始水平;类似地，从某个压力p >提升到Po的包裹将具有负浮力，也倾向于返回到它来自的地方。当大气均匀时，I/cp是恒定的，人们可以通过将两者绝热降低到标准压力po并比较那里的密度来确定压力pi下的包裹在绝热位移到p2时是否具有浮力。换句话说，对于一个均匀的大气，人们可以立即从一个相对于po的势密度图中看出哪些区域是稳定的，哪些区域将趋向于翻转。当大气不均匀时，情况就不同了。当一个密度为p(pi)的包裹位移到p2时，如果

继续阅读:辐射平衡的基本模型

这篇文章有用吗?

0 0