范德瓦耳斯方程

正如我们前面学到的,近似的理想气体工作如果我们可以忽略分子间作用力。这是主要几乎总是如此成分的空气在类似地球的条件。但作为一个气体接近其临界温度和液体或固体可以与气相共存,偏离理想是很重要的。从图5.2我们看到理想气体状态方程描述的行为真实气体在高温和低压力的极限情况。等温线对理想气体是矩形双曲线(p 1 / V)。一个小压力降低导致大量增加体积在图5.2 (B)。然而,理想气体状态方程不再是一个好的近似时气体的温度低于其临界点,和等温线的体积范围内成为水平(见平段C B在图5.2);即。,有一个混合的液体和气体处于平衡状态。

一种非常有用的方程,描述了许多物质的行为范围广泛的温度和压力是范德瓦耳斯派生的。1摩尔的气体的范德瓦耳斯方程是:

范德瓦耳斯方程(5.2)

在a和b是常数(不同不同的物质)和v是气体的摩尔体积(即。,减少体积或特定的体积)。术语b(5.2)是由于有限的大小分子,尽管这个术语/ v2是由于分子间作用力有吸引力的影响。= b = 0,范德瓦尔河方程减少理想气体定律(5.2)。

范德瓦耳斯方程通常是书面形式

图5.4显示了一个示例的等温线使用范德瓦耳斯方程计算。如果我们比较图5.2和5.4,我们发现范德华等温线

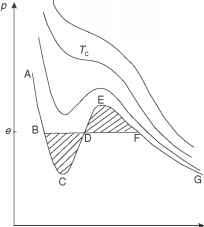
图5.4范德华等温线。拐点的等温线是关键的等温线。平衡蒸汽压e是这样阴影区域是相等的。

图5.4范德华等温线。拐点的等温线是关键的等温线。平衡蒸汽压e是这样阴影区域是相等的。

繁殖许多真实气体的行为特点。如图5.4大v和低p有大量增加体积小的减少压力。液体(小v和高p)有一个小体积的减少,大量增加的压力。有一个关键的等温线随温度T = Tc表明拐点(d2p / dv2 = 0)的等温线温度高于Tc非常类似如图5.2所示。然而,等温线随温度小于Tc看起来非常不同:他们不是水平在该地区的两个阶段,水和蒸汽,共存。考虑一个特定的等温线英语字母来自范德瓦尔斯方程。让我们压缩气体,直到饱和发生点F等温线。然后进一步降低音量没有压力的增加,相对应的水平伸展FB。相反,范德瓦耳斯等温线显示压力的增加(图FE)的一部分。在这个分支曲线的过饱和蒸汽。 Vapor can theoretically exist for these values, but if a small impurity is present such as a dust particle, or a scratch on the wall, the vapor will begin to condense on this site and the system will collapse to the flat horizontal line BF in Figure 5.4. In other words this state of the vapor is unstable: any disturbance causes it to migrate to a stable condition which contains two subsystems, vapor and liquid. So, if we plot the van der Waals isotherm for a given temperature, we will not find the flat portion (BDF) which we know should be there (from experiment). We have to put it in "by hand." But how do we decide the proper pressure value at which to insert this flat portion? The rule (first discovered by Maxwell) is that the areas bounded by the curves BCDB and DEFD have to be equal. Let us sketch a proof. Consider the cycle FEDCBDF in Figure 5.4

(“图8”的一面)。第一定律我们知道的一个等温过程所做的工作在一个封闭的周期等于被系统吸收的热量,AW = AQ,因为内部能量的变化是零循环过程。我们也知道循环积分dQrev / T = 0(我们的过程的可逆的)。对于一个等温过程,我们可以把温度的积分,得到Qloop = 0。自从Qloop = 0,我们也有Wloop = 0。如果没有这样的水平线的领域是相等的,我们的假想(但可实现的)过程将违反热力学定律(dU = 0或¡f dS = 0或两者)。

一个优秀的不稳定状态的讨论(过饱和等)可以在先进的书籍,特别是讨论Callen(1985),在与范德瓦尔斯系统说明了情况。1稳定的标准可以表达的凹面或凸面的热力学函数:

	d 2 s		d 2 s
	d U 2	> 0,	d V2 > 0	(稳定性判据)
和吉布斯能量:
	d 2 g		d 2 g
	d T 2	< 0,	dG < 0	稳定性判据。

如果年代的图表(U, V, M)和G (T, p M)错误的凹面的迹象的分支曲线标准失败将不稳定的地方。

继续阅读:信息Ixl

这篇文章有用吗?

0 0