Dn3
通过重复相同的理由所有封闭的轮廓,一个潜在的涡度的结论是统一定义的域内最外层的封闭的潜在的涡量等值线。最后,我们注意,如果水不移动,涡度不是均质。
注意潜在的涡度均化取决于小down-gradient耗散的假设。潜在的解决方案与一个不通风的层vor-ticity被均质化后可以很容易找到,如下。表示的西部边界阴影区东部第三层为美联社。美联社第三层是静止的,所以只有一个移动层。美联社以西潜在的涡度是均质在第三层。因为潜在的涡度应该沿着线从P是一个常数,这个常数等于沿着北部边界涡量的潜力。因此,第三层厚度h3 = fh3e (4.203)
纬向动量方程第二和第三层是d
3一个cosBdk
P4 - P3, P4 - P2, g3 = g - Y3 = (4.206)
斯维德鲁普关系两层cos0 (h2v2 + h3v3) =一种罪恶防波堤入口(4.207)
结合这三个方程,得到一个积分层厚度的关系
(Y3 - 1) h2 + (h2 + h3) 2 = + (Y3 - 1) h2e + (h2e + h3e) 2 (4.208)
结合Eqn。(4.203),可以计算出层厚度h2和h3。速度场可以从地转状态计算。
为了简化问题,我们讨论的第一层露头模型的边界南部盆地南部;因此,实际上没有图层1在我们的域模型。在下面的讨论中,我们将调用层2上层,目前覆盖整个盆地模型,和第三层将被称为“底层”。两层的厚度沿东部边界设置为500。的密度分层和埃克曼泵领域保持前面讨论过的一样。
解决方案的结构Figure4.35所示。它随时可以看到解决方案包括两个动态域由潜在vor-ticity同质化的东部边界地区较低的层,可以很容易地确定为域
-
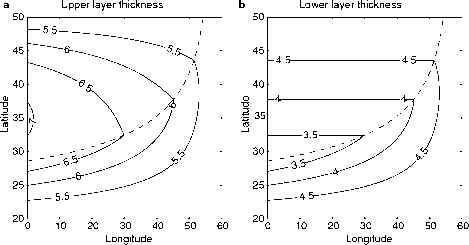
- 图4.35上和b下层厚度(100)21/2-layer通风温跃层模型。
纬度较低的层厚度是独立的西北(图4.35 b)的一部分。建设解决方案如下。使用命令。(4.203)和(4.208),我们可以计算域内的解决方案的潜在涡度较低的层的均质化。正式使用这个方法,我们可以计算出总分配层厚度h = h2 + h3,和东部边界的领域潜在的涡度均化的什么地方h = h2e + h3e是因为这条线以东较低的层是停滞不前,所以较低的界面应该是平的。
第三层是运动时,斯维德鲁普通量的一部分现在分成第三层。因此,在潜在的涡度均化区在第三层,第二层的体积通量降低,所以界面变形。例如,在目前的情况下,2层的厚度约460 46岁°N和西部边界附近(图4.35);然而,相应的层厚度的情况下没有封闭轮廓的第三层略大于700 m(图4.30 b)。东的封闭地转轮廓较低的层,层厚度这两层是完全相互补偿,表明平界面层2以下。
通风温跃层的基本特性
通风温跃层理论,结合潜在的涡度均匀化理论,提供了一个严格的框架在中纬度海洋风力循环。它已成为现代风力循环理论的理论基石。理论的最重要的特征和发展超越了其最初的形式总结如下。
的基本结构通风温跃层
海洋风力循环上公里由以下主要部分组成:
•的埃克曼层在上面,这是直接接触大气强迫,包括风应力、热通量和淡水通量。这一层的角色形成水包裹与合适的密度和抽成地转流下面的政权。
•埃克曼层下面的地转政权由几种政权具有明显不同的动力学:
•通风温跃层,水包裹直接暴露于大气强迫在露头为每个在冬末的等密度的窗口。南部的露头线,水在通风层包裹俯冲进入地下海洋,他们继续他们的运动由斯维德鲁普动力。特别是,单个水包裹的潜在涡度守恒沿着它的轨迹。
•阴影区,水是停滞不前的框架内的通风温跃层。当然,水可以设置在运动的一部分,在世界各大洋温盐环流,但这超出了本文的范围通风温跃层。
•池政权或潜在的涡度均质政权,在潜在的涡度设定的过程是通过Ekman抽通风。
超出了简单的通风温跃层:
•海表面密度ps指定先验的晚冬的价值。评论:没有季节性周期的模型。这种假设是基于Stommel恶魔,也就是说。,模型是迫于晚混合层属性。另一种方法是通风温跃层模型耦合到混合层与季节性周期,ps可以确定同时作为解决方案的一部分(例如,马歇尔和培育者,1991;刘和Pedlosky, 1994)。然而,一些复杂的非线性过程,如在冬末的对流调整,很难处理在一个分析模型,这仍然是最具挑战性的问题之一。
•埃克曼泵被指定为上边界条件,因此,埃克曼通量计算风力循环作为一个单独的组成部分。评论:一个可以选择指定风应力的上边界条件。这样,埃克曼通量计算作为上层流动的一部分,因此,解决方案可能看起来不同于从以前的配方。
•液体被假定为理想流体。因此密度、潜在的涡度和伯努利俯冲后沿着轨迹函数是守恒的。备注:基于水文观测数据分析表明,混合在海洋呈现密度流线,潜在的涡度,和伯努利功能保守。然而,结果从一个ideal-fluid-based模型可以提供有用的见解调节循环的物理机制。
•没有界面质量流量被允许在原始模型。备注:界面质量流量可以包括,其包含一个简单的方法来研究风力循环之间的相互作用和温盐环流。然而,这个问题所需的机械能维持密切相关的垂直混合分层海洋,涉及复杂的动力学过程,将在后面的小节中讨论。
•不包含在原始模型混合层。事实上,艾克曼层被认为是无限薄的上表面通风温跃层模型置于z = 0。评论:这是一个重大的财政赤字在原始模型,因为所有通风层被迫露头沿着东部边界和零厚度。因此,东部边界出现的奇异线模型。此外,零厚度的假设混合层可以大幅扭曲风动环流的结构。然而,amixed层指定的有限厚度可以添加和先天的上边界条件。这将是连续的情况下讨论分层模型。
•分层沿东部边界必须被指定。备注:这是一个基本假设的理想铃温跃层理论。失重的情况下模型用一个移动层,需要指定层厚度作为一个外部参数;因此,可想而知,一个模型与n层应该要求规范移动沿着东部边界的n层的厚度。
•东部边界附近的阴影区是一个独特的特性,在通风温跃层模型。阴影区域的边界是一个流体的特征源于露头线和东边界之间的十字路口。每次这种特性满足新的露头线,它分裂成两个特点,分离流进区域潜在的涡度函数有不同的结构。区与不同数量的动态(潜在的涡度的函数)双打每次遇到新的露头线特征。因此,随着通风层数的增加,通风温跃层的复杂性成为指数。
•的域模型是适用于海洋仅限于海洋内部,远离西方的边界和再循环机制。模型的基本限制的模型是基于线性斯维德鲁普动力,不包括摩擦效应和非线性平流项。
•模型不能用于西部边界政权应该包括其他高阶动力学。备注:简单的摩擦边界层不能匹配到通风温跃层模型产生一个封闭的循环在一个盆地,因为复杂的动力学和热力学过程发生在混合层是省略了从模型;因此,从西方的外缘边界流线与露头的流线中期海洋,远离西部边界。
•再循环的模型是无效的非线性平流项变得居多的重要制度。备注:所有模型基于线性内斯维德鲁普动力失败再循环机制。再循环的动态机制仍然是海洋动力的主要挑战之一。
4.1.8多层惯性西部边界电流
惯性西部边界电流与两个移动层
后成功解决目前单层惯性的西部边界,是尝试找到解决西方two-moving-layer惯性边界电流;然而,在这个方向上努力经历很挣扎。布兰德福德(1965)发现分析解决方案的情况下潜在的涡度是恒定在两个移动层;然而,他的解决方案表现出一个意想不到的分离在纬度从single-moving-layer模型比这低得多。
基本上,他发现two-moving-layer惯性的西部边界方程系统当前层是坏脾气的(有时也称为“僵硬的方程系统”)。困难在处理所谓的坏脾气的方程如下。很快将被解释,当潜在的涡量是恒定的,一般的解决方案惯性西部边界层坐标以指数函数的形式,如exp (±kix)。由于边界层的解决方案必须发现匹配他们内部解决方案在无穷远处,指数的解决方案与大ki可以迅速增长,因此很难处理数值。尽管他使用最好的数字包可用,他无法找到顺利的解决方案独立于西方在纬度预期从single-moving-layer模型边界。这个问题仍然没有解决了20年。
Luyten和Stommel(1985)解释了矛盾的情况的虚拟控制首先发现于一维水力问题,森林(1968)。Luyten -Stommel模型是基于一个假设的零电位涡度是不现实的。因为相对涡度是可以忽略不计的内部解决方案,减少潜在的涡度的形式/ h;zero-potential-vorticity解决方案可以追溯到backupstream到一个地方与f = 0(赤道)或h = < x(无限层深度)。如在这一节中所讨论的,然而,与西方惯性边界层相关的困难可以解决一般情况下的非零潜在的涡度。事实上,使用流函数坐标变换降低了坏脾气的微分方程系统运转良好的系统,可以很容易解决。
模型公式
类似于一个惯性的情况下西部边界与单个移动当前层,一个模型的基本方程与22层包括地转条件cross-stream动量方程,ageostrophic条件下游动量方程,连续性方程为两层。j-plane这些方程
U1V1x + V1V1y + fU1 = - g ' (yh1y + h2y) (4.210)
在g ' = g (p3 - P2) / p和y = (p3 - p \) / (p3 - P2);和px, p2和p3的密度(顶部),第一层第二层,和最低层,这被认为是非常厚,一动不动。
系统处于semi-geostrophy因为下游速度由cross-stream geostrophically平衡压力梯度,但cross-stream速度遵循ageostrophic约束。潜在的涡度方程可以推导两层,cross-differentiating并减去相应的动量方程:
继续阅读:Pp QB p
这篇文章有用吗?
