信息Gjf
1rTir"i"T"illllq,"il"r"i 20 30
经度
I雷竞技csgo111 ! 111 ! 111 ! 111 ! 111 ! 111 ! 111 ! 111 !10 10 20 30 40 50 0 10 20 30 40 50
经度
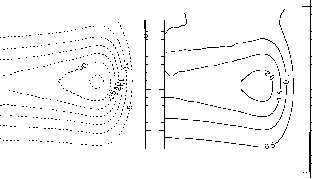
图4.62反常Ekman泵送引起的扰动,如图4.61所示:地表高程(cm);B表面密度(kg/m3);C深度a = 27.0 kg/m3等流面(m);D风驱动环流的深度(单位为100米)。
1rTir"i"T"illllq,"il"r"i 20 30
经度
I雷竞技csgo111 ! 111 ! 111 ! 111 ! 111 ! 111 ! 111 ! 111 !10 10 20 30 40 50 0 10 20 30 40 50
经度
图4.62反常Ekman泵送引起的扰动,如图4.61所示:地表高程(cm);B表面密度(kg/m3);C深度a = 27.0 kg/m3等流面(m);D风驱动环流的深度(单位为100米)。
4.4再循环
4.4.1的动机
我们的讨论仅限于基于内部Sverdrup动力学和西部边界流的模型,这些模型与沿西部边界的内部解匹配,包括与西部边界区域南半部的内部解匹配的惯性西部边界流的情况。在这个理论框架内,最大流函数完全由从盆地东部边界开始的Ekman抽速的带状积分决定。然而,观测结果表明,墨西哥湾流的最大体积通量约为150 Sv,比从Sverdrup关系中计算出的值大几倍(图4.63)。
-
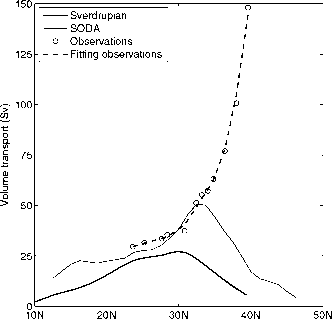
- 图4.63墨西哥湾流输运的比较:观测数据(圆)、拟合观测数据(重虚线)、低分辨率模型(SODA)(细实线)和风应力计算的Sverdrup输运(重实线)。
线性Sverdrup动力学分析表明,环流的体积输运在佛罗里达海峡纬度处达到最大值,然后在该纬度段逐渐减小更高的纬度.另一方面,观测到的输运比Sverdrup动力学的输运要大得多。即使在佛罗里达海峡的纬度,观测到的输送比斯维德鲁普动力的输送要大。在40°N附近,观测到的输运达到最大值150 Sv (Gill, 1971),但Sverdrup动力学预测的输运几乎为零,因为这里接近零风应力旋度纬度。在北太平洋也有类似的现象,在那里黑潮延伸及其动力学和变异性已被广泛研究(全面回顾,见Qiu, 2002a)。
线性理论和观测之间的差异是由于两个因素。首先,在常用的线性理论中,为了简化分析,水平动量方程中的惯性项被忽略了。如上所述,惯性项在强边界流中至关重要,如墨西哥湾流、黑潮和ACC。副热带环流西北(西南)角有再环流区北半球(南半球)其中循环是强非线性的。其次,与地形上的分层流动有很强的相互作用,这被称为底部压力扭矩或JEBAR(斜压性和底部起伏的联合效应)术语,这在第4.4.5小节“底部压力扭矩的作用”中详细讨论。
由ai°x 1°低分辨率模式(SODA)诊断的西部边界流输运可以清楚地看到JEBAR项的贡献。这样的模型不能模拟涡流的影响。然而,在34°N附近,反气旋环流的输送超过50 Sv。
在本节中,我们将讨论再循环的初步理论。大多数已发表的关于中尺度涡旋在环流中的作用的理论工作都是基于准地转理论。此外,底部压力扭矩的作用可以在不显式调用涡流的情况下进行解释;因此,底部压力扭矩的含义将使用一个简单的非涡解模型的结果来解释。这类模型的潜在缺点将在本节的末尾进行评论。
4.4.2 Fofonoff溶液
对于单运动层模式,拟地转涡度方程为
J (f, + Py) = ffw - RV2f (4.344)
其中R ^ O(1)为摩擦参数。Fofonoff(1954)建议寻找没有强迫和摩擦的解决方案。因此,我们将埃克曼泵浦和摩擦均设为零(R = 0);由于位涡量是守恒的,这样的解应该满足涡量守恒定律
其中F(F)是F的任意函数。
正如Fofonoff(1954)首次讨论的那样,有许多不同的解决方案。然而,这些解中有许多与海洋内部环流无关,因此需要找到满足Eqn的解。(4.344),是整个盆地的有效解。
整合Eqn。(4.344)在封闭流线内的区域Af上导致积分约束ffA f0Wfy) = R$C* u- dl (4.346)
这个约束可以用来找到问题的解决方案;然而,这并不是一件容易的工作。找到这个问题的解的一种方法是假设这个函数F(F)的某种简单形式,从而得到与这个约束一致的解(Niiler, 1966)。作为一个例子,我们假设这个函数是这样的
内部解决方案
在海洋内部,惯性项即相对涡量可以忽略不计;因此,由Eqn。(4.347)解是fi = y - y0 (4.348)
它代表了一个向西的匀速气流。为方便起见,我们选取南部边界为y0 = 0,因此沿模型盆地南部边界没有边界层。
很明显,在盆地的其他边界上,由内部解计算的流函数不为零,fI = 0。为了满足零流函数的边界条件,在所有其他边界上都必须存在边界层。在西边界x = 0处。让我们把流函数分成两部分:
替换命令。(4.348,4.349)变成Eqn。(4.347),得到
在西部边界内,y导项比x导项要小得多,所以这个方程在xd2中被简化为常微分方程
满足边界条件fw (0) = - fi,和fw ^ 0,在x ^
其解是fw = -ye-^x (4.353)
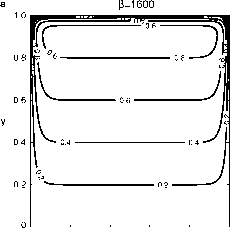
沿x = 1和y = 1处边界的边界层解具有类似的结构;因此,完整解为f = y h - e-^x - e-^(1-x)] + e- vp (1-y) (4.354)
两种方案如图4.64所示。
继续阅读:太平洋在西半球吗
这篇文章有用吗?
