定向发射率
发射率取决于发射的方向(见1.4秒。),这就是为什么我们合格发射率前面讨论的兴趣作为正常的发射率。对于一个不透明的身体,吸收率辐射在一个特定的方向是1减去反射率,发射率由基尔霍夫定律。因为反射率取决于方向发射率。图1.13显示了纯水的反射率与入射角未极化的入射辐射(= 10点)和相应的发射率计算使用菲涅耳系数(7.2秒。)。在这个波长,只有几毫米厚的一层水是不透明的。如果发射率取决于方向,所以必须亮度温度。
亮度温度结核病被定义为在一个方向
J e (u, d)体育(u, T)杜+ J {1 -£(u, d)} Pe (u, Ts) du = J Pe杜(u, Th), (1.65)
集成的范围是由仪器,e (u,■&)光谱emis-sivity T方向(热力学)温度,和Ts是天空的亮度温度(这也取决于方向;见2.2秒。)。左边第一个积分Eq。(1.65)排放;第二个积分是反射的辐射的天空。就是明证的依赖程度低(正常)发射率的水在频率范围(图1.12),我们可以忽略情商的定向辐射的频率依赖性。(1.65)。因为我们的红外测温仪响应一个狭窄的范围(约下午2点)的波长大约10点,我们可以近似的Eq。(1.65)
频率对应于10点。我们还假设反射与排放相比可以忽略不计,这对于near-glancing角度是不正确的。在这个波长,T 300 K左右,普朗克函数的指数项情商。(1.11)远远大于1,因此我们可以近似Eq。(1.66)
£exp(胡/ kBTb)«exp(胡/ kBT) (1.67)
两边取自然对数和重新排列得到胡锦涛胡锦涛kBTb kBT
如果我们写结核病= T -,假设在C / T 1,我们可以进一步的近似Eq。(1.68)
T -结核病kbt, n
T胡
因此我们预测,在一个固定的温度T,热力学温度T和亮度温度之间的相对差异结核病对任何方向是负的自然对数的线性函数的方向发射率。
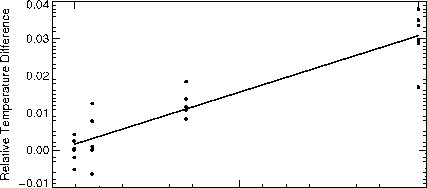
验证情商的正确性。(1.69)我们测量水的亮度温度在30厘米x 40厘米约2厘米深的锅在四个海拔角度(60°,40°,25°,16°)。因为红外线温度计无法区分发射和反射辐射,水被加热到最大化排放,和测量是凉爽,晴朗的日子里从天空入射辐射降到最低。从图1.13辐射率了。Eq。(1.69) T是水面的温度,而由于蒸发冷却,不是一个沉浸一个普通的温度计在水措施。作为一个很好的估计T我们使用了亮度温度60°(平均);这个方向的发射率接近1(图1.13)。发射从头顶的天空与亮度温度低于约218 K天测量(见2.2秒。更多关于天空的亮度温度的变化方向)。的
仰角(度)60 40 25 16
仰角(度)60 40 25 16
0.00 0.04 0.08 0.12 0.16
ln(辐射)
图1.14:测量热力学温度和亮度温度之间的差异相对于纯水的热力学温度四个高度角六每角测量。直线是一个线性最小二乘适合测量。卡方拟合优度统计量是0.00065意味着相关系数r2为0.83。
0.00 0.04 0.08 0.12 0.16
ln(辐射)
图1.14:测量热力学温度和亮度温度之间的差异相对于纯水的热力学温度四个高度角六每角测量。直线是一个线性最小二乘适合测量。卡方拟合优度统计量是0.00065意味着相关系数r2为0.83。
反射率的水从头顶的天空辐射小0.01)。我们做了六套测量四个方向。水的表面平均温度约为338 K,边坡的Eq(1.68)约为0.22。图1.14显示了一个最小二乘适合所有的测量,与预测边坡坡度为0.22,在协议即使所有的近似,使测量的困难。我们有更多的关于定向发射率在2.2节。
继续阅读:吸收截面
这篇文章有用吗?