恒压差过滤

当悬浮液上方的空间受到压缩气体或滤板下方的空间处于真空过滤在恒定的压差下进行(接收器内的压力是恒定的)。的过滤速率由于滤饼厚度增加，流动阻力减小。一个类似的过滤过程的结果，由于压力差的悬浮层的静水压恒定厚度位于过滤介质．

如果悬浮液以恒容量的往复泵送入过滤器，则在恒流量下进行过滤。在这种情况下，压差由于饼阻力的增加而增加。如果悬架是由a离心泵时，其容量随滤饼阻力的增大而减小，在变量下进行过滤压力差异和流量。滤饼形成的最有利的过滤操作是不发生过滤介质堵塞的过程。在悬浮液中固体颗粒浓度足够高时，可以观察到这种过程。从实际的角度来看，可以有条件地假定该浓度超过体积的1%。过滤经常伴随着固体颗粒的受阻或自由重力沉降。重力和滤液运动的相对作用方向可以是同时的，逆流或交叉电流，取决于过滤板的方向，以及污泥的位置上方或下方的过滤板。重力和滤液运动的不同方向与滤饼、悬浮液、滤液和清液的分布情况如图1所示。颗粒沉降使过滤过程复杂化，并影响控制机制。此外，这些影响取决于重力和滤液运动的相对方向。如果悬浮液在过滤介质上方(图1A)，颗粒沉降导致更快速的滤饼形成与一个清晰的滤液，可以从过滤器通过倾析．如果悬浮液在过滤介质下(图IB)，颗粒沉降将防止饼的形成，有必要混合悬浮液以保持均匀性。

^ vvyvVvvAVgi j

?
年代
•我
我
>	v:
年代	h
>
＊
§
>
1	＊

图1。滤芯重力作用方向及滤液运动方向:a -并流;B-countercurrent;C-crosscurrent;实心箭头方向重力作用力作用;虚线箭头-滤液运动方向;1-filter板;2-cake;3-sludge;4-filtrate; 5-clear liquid.

当饼结构由易于变形或在压力下重新排列的颗粒组成时，所得到的饼的特征是可压缩的。那些不容易变形的被称为半可压缩的，而那些只有轻微变形的被认为是不可压缩的。孔隙率(定义为孔隙体积与饼的体积之比)不随压降的增加而减小。可压缩滤饼的孔隙度在压力作用下减小，其对液相流动的水力阻力随着压差的增大而增大过滤介质．

含有沙粒的饼无机物质超过100pm的尺寸可能被认为是不可压缩的。不可压缩的蛋糕形成材料的例子是沙子和碳酸钙和钠的晶体。含有颗粒的蛋糕金属氢氧化物，如氢氧化铁、氢氧化铜、氢氧化铝，以及由初级细晶体形成的易变形团聚体组成的沉积物，通常是可压缩的。在滤饼形成完成后，滤饼的处理取决于特定的过滤目标。例如，饼本身可能没有价值，而滤液可能。根据处置方法和颗粒的性质，饼可以以干燥形式丢弃，也可以作为浆液丢弃。在这两种情况下，蛋糕通常都要进行清洗，要么在它形成后立即清洗，要么在干燥一段时间后清洗。在某些情况下，需要第二次清洗，然后是干燥期，其中所有可能的滤液必须从饼中去除;或在湿法排放后处理:或在重新制浆和第二次过滤发生;或者干饼处理更可取。如果滤饼有价值且必须去除所有污染液体，或者滤饼和滤液都有价值，则采用类似的处理方案。在后者，饼形成过滤采用，不洗涤，对饼脱水，无价值的，不污染的液体形成残余悬浮液在饼。 To understand the dynamics of the filtration process, a conceptual analysis is applied in two parts. The first half considers the mechanism of flow within the cake, while the second examines the external conditions imposed on the cake and pumping system, which brings the results of the analysis of internal flow in accordance with the externally imposed conditions throughout. The characteristics of the pump relate the applied pressure on the cake to the flowrate at the exit face of the filter medium. The cake resistance determines the pressure drop. During filtration, liquid flows through the porous滤饼沿水压梯度减小的方向。孔隙度(e)在滤饼与滤板接触点处(即x = 0处)最小，在滤饼表面(x = L处)最大，当污泥进入时。这个系统的示意图定义如图2所示。

下标我

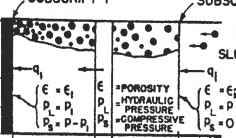
图2。饼形成的重要参数。

下标我

下标我

泥浆

图2。饼形成的重要参数。

施加在每个粒子上的阻力传递给相邻的粒子。因此，随着滤板的靠近，净固体压缩压力增大，导致孔隙率降低。参考图3A，可以假设粒子只在其表面的某一点接触，并且液体完全包围着每个粒子。因此，液体压力在垂直于流动方向的平面上均匀地起作用。当液体流过每个颗粒时，力的法向分量的积分产生形式阻力，切向分量的积分产生摩擦阻力。如果粒子是非球形的，我们仍然可以假设相邻粒子之间的单点接触，如图3B所示。

考虑通过滤饼(图3C)的流动，膜位于距离滤板x的位置。忽略饼中除了阻力和水压产生的力外的所有力，从x到L的力平衡为:

施加的压力p是时间的函数，而不是距离x的函数。Fs是粒子上的累积阻力，在x = L到x = 0的方向上增加。由于假设是单点接触，因此液压pLis有效地覆盖了饼的整个横截面(A);例如，针对图3B所示的虚拟膜。式1除以A，用压阻压力ps= F/A表示，可得:

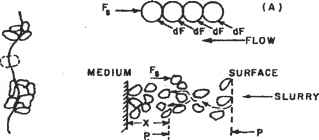
图3。可压缩饼中颗粒的摩擦阻力。

图3。可压缩饼中颗粒的摩擦阻力。

地面是一个虚构的压力，因为横截面积既不等于颗粒的表面积，也不等于实际接触面积。在实际饼中，有一个小的接触面积，施加在固体上的压力可以定义为Fs/Ac。

在蛋糕内部求关于x的微分，我们得到:

这个表达式表明，当流体从滤饼的外表面向滤板移动时，阻力压力增加，液压压力降低。根据达西定律，当孔隙率(e)和比阻(a)一定时，水力压力梯度沿滤饼呈线性变化。这样就可以认为饼是不可压缩的。这可以用图4中单位过滤器面积流量与压降的关系图得到的直线来说明。孔隙率和比阻的变化伴随着不同程度的压缩性，如图4所示。

过滤过程的速率与驱动力成正比，与阻力成反比。

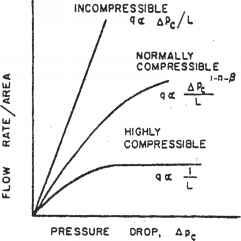
图4。整个滤饼的流量/面积与压降的关系。

由于滤饼和过滤介质的孔径较小，通过孔隙的液体流速较低，可以认为滤液流动为层流，因此适用泊肃叶定律。滤速与压差成正比，与流体粘度成反比，与滤饼和过滤介质的水力阻力成反比。由于滤饼和滤料的压力和水力阻力随时间变化，因此可变过滤速率可表示为:

dV Adx

式中V =滤液体积(m3) A =过滤面积(m2) t =过滤时间(sec)

假设滤道中存在层流，由力平衡得到的过滤基本方程为:

一个dT

其中Ap =

压差(N/m2)滤液粘度(N-sec/m2)滤饼阻力(m"1)初始过滤阻力(滤板和滤道的阻力)(m"1) u =滤速(m/sec)，即滤液通过滤饼和滤板的流量dV/dx =滤速(m3/sec)，即滤液流速

滤饼阻力(Rc)是单位面积过滤滤液流动的阻力。滤饼厚度越大，Rc值越高。在任何时刻，Rc取决于由于V (m3)滤液的通过而沉积在滤板上的固体质量。Rf可以假定为常数。要确定体积与停留时间t的关系，必须对式5进行积分，即Rc必须用V表示。

我们用x^表示滤饼体积与滤液体积之比。因此饼的体积是x^V。饼体积的另一种表达式是hcA;其中hc为模饼高度，单位为米。结果:

因此，滤饼均匀分布在滤板上的厚度为:

滤饼阻力可表示为:

式中r0=比体积饼电阻(m"2)。

由式8可知，r0表示厚度为1m的饼对液体流动的阻力。

将式8中的Rc代入式5，可得:

滤液体积Xq可以表示为滤板上固体颗粒的质量与滤液体积的比值(xw)，用特定的质量饼阻力rw代替r0。即r w为均匀分布的饼产生的流动阻力，单位为1kg /m2。用质量代替体积单位，式9中的r0 Xq变为rwxw。忽略滤板电阻(Rf = 0)，考虑式7，由式3可得:

当fn= 1 N-sec/m2时，hc = 1 m, u = 1 m/sec, r 0 = Ap比饼阻力等于粘度为1n秒/m2的液相以1m /秒的线速度通过1m厚的滤饼所需要的压差。然而，这个假设的压差超出了实际范围。对于高压缩性蛋糕，r0可以超过1012m2。假设V = 0(在过滤开始时)，滤板上没有滤饼。公式9变成:

当^ = 1 N-sec/m2, u = 1 m/sec时，Rf = Ap。这意味着滤板阻力等于液相(粘度为1 N-sec/m2)以1 m/sec的速度通过滤板所必需的压差。对于许多滤光片，Rf通常为1010米“1。

对于定压降和定温过滤过程，除V和t外，式9中的所有参数均为常数。对式9积分0到V的极限，从0到t，可得:

V x

Wo J^ + VRfV = APAx

等式两边除以±jlï^IK得到:

V2 + 2

RfA)

yJ2LPA * \

roxo,

式13为过滤时间与滤液体积的关系。这个表达式既适用于不可压缩饼，也适用于可压缩饼，因为在恒定Ap下，r0和Xq是常数。如果我们假设有一个确定的过滤装置，并设置一个恒定的温度和过滤压力时，则Rf、r0、fi、Ap值为常数。 公式13中括号中的项被称为“过滤常数”，通常被合并为参数K和C;地点: 因此，可以写出一个简化的表达式来描述过滤过程: 过滤常数K和C可以通过实验确定，由此可以计算出在一定时间间隔内(对于某种过滤器，在相同的压力和温度下)获得的滤液体积。如果改变工艺参数，由式14和式15可估计出新的常数K和C。式16可以进一步简化，将x0表示为依赖于K和C的常数: 将Tq代入式16，恒压过滤方程为: 式18定义了滤液体积与时间的抛物线关系。该表达式对任何类型的饼都有效(即，可压缩和不可压缩)。从V + C对(t+t0)的图中，过滤过程可以用抛物线表示，其顶点在原点，如图5所示。将轴移动到距离C和t0，提供了系统在体积与时间方面的特征过滤曲线。由于抛物线的顶点并不位于这个新系统的原点，这就很清楚为什么在过程开始时的过滤速率会有一个有限的值，这与实际情况相对应。 (v + c)2 = k (t + t0) 图5。典型的过滤曲线。 方程18中的常数C和x0有物理解释。它们基本上相当于一层具有相同阻力的虚拟蛋糕。这个虚拟饼的形成遵循同样的抛物线关系，其中x0表示形成这个虚拟质量所需的时间，C是所需滤液的体积。微分方程16给出: 以互惠关系的形式重新安排: dx_ = 2V + 2C dV K + K 这种形式的方程提供了如图6所示的线性关系。这个表达式是斜率为2/K，截距为c的直线的表达式。通过这个表达式的函数形式，dx/dV的实验测定变得很简单。应按时间间隔t和t2测量滤液体积V和V2。那么，根据式16: Y22 - vf + 2c (v2 - 2 c K 在检查这个表达式的右侧时，我们注意到商等于获得滤液体积时刻速率的倒数，它等于体积V和V2的平均算术值: 过滤常数C和K可以根据对不同时间间隔的滤液体积的多次测量来确定。 dv博士 图6。方程20的曲线。 图6。方程20的曲线。 由式14和式15可知，C和K的值取决于滤饼比体积阻力r0, r0又取决于滤饼上的压降。这种Ap，特别是在过滤的初始阶段，在滤饼中经历变化。当滤饼很薄时，总压降的主要部分作用在过滤介质上。随着蛋糕变厚，通过蛋糕的压降迅速增加，但随后趋于稳定。等压过滤与式16的偏差不显著。为了进行近似计算，只要滤饼不是太薄，就可以忽略滤板的阻力。则式15中滤板电阻Rf = 0，式15中C= 0，式17中t0 = 0。因此，过滤简化方程为: 对于厚饼，式23的结果与式16的结果接近。

继续阅读:滤料过滤公式

这篇文章有用吗?

0 0