Fci fcj
删除一个估计。
旨在带宽可以被视为一种折中小h(大方差和小偏差)和大型h(小方差和大偏差)。
- | |我)我| | | \ | | -800 1000 1200 1400 1600 1800 2000 2200
一年
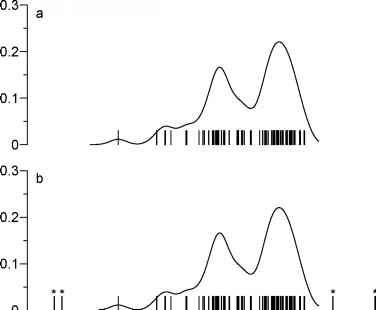
图6.4。易北河冬季洪水、pseudodata一代。沉重的事件(大小2 - 3)从完整的记录(图1.1)和策划(a, b)酒吧(m = 73)。“两点”规则用于生成四pseudodata点(b,星号)外的观测时间间隔。出现率与h = 35,估计也没有(m) = 73)或(b) = 77) pseudodata。
- | |我)我| | | \ | | -800 1000 1200 1400 1600 1800 2000 2200
一年
图6.4。易北河冬季洪水、pseudodata一代。沉重的事件(大小2 - 3)从完整的记录(图1.1)和策划(a, b)酒吧(m = 73)。“两点”规则用于生成四pseudodata点(b,星号)外的观测时间间隔。出现率与h = 35,估计也没有(m) = 73)或(b) = 77) pseudodata。
6.3.2.5例子:冬天易北河洪水(继续)
重的数量(大小2 - 3)在冬天易北河的洪水是m = 73。第一个事件是在1141年。然而,分析了历史信息追溯到1021年(Mudelsee et al . 2003年),和观测时间间隔(1021;2002)。Pseudodata代(图6.4)使用的“两点”的规则(气候和其他)的趋势在洪水风险边界。
交叉验证函数(图6.5)有一个最低的h = 41。抑制潜在的外推效果(6.3.2.3节)和进一步减少偏差(6.3.2.4节)顺利,也许是明智的。因为这个原因和实现一致性的结果来自其他洪水记录(易北河,夏天;奥得河,冬季和夏季),Mudelsee et al。(2003)设置分析带宽h = 35。估计洪水出现率(图6.4)上的沉重
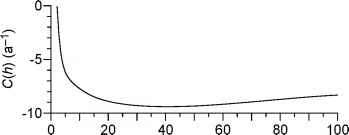
图6.5。易北河冬季洪水、交叉验证功能,沉重的事件(大小2 - 3)。
图6.5。易北河冬季洪水、交叉验证功能,沉重的事件(大小2 - 3)。
冬季洪水Elbe-little边界的偏见。原因是发生速度边界相当低。
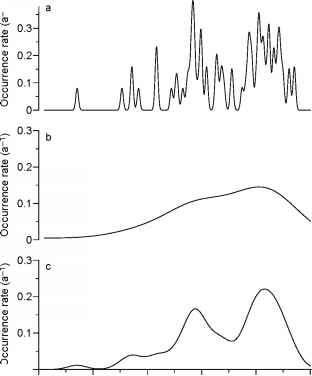
带宽选择有大量对洪水的影响出现率估计。太强劲undersmoothing h = 5(图6.6)允许太多的变化。在引导信心乐队(6.3.2.6节),大多数的摆动是不重要的(没有显示)。太强劲oversmoothing h = 100(图6.6 b)降低了估计方差,但增强了偏见:太多重大洪水发生的变化速率平滑。适量的平滑似乎表明通过交叉验证;一个只有轻微undersmoothing h = 35(图6.6摄氏度)让出现重大变化。沉重的冬天易北河洪水的例子是在部分6.3.2.7进一步追求。
6.3.2.6引导信心乐队
测量的不确定性(T) (Eq。6.33)解释结果至关重要。例如,它可能被问到在T (T)低1700 w沉重的冬天易北河的洪水(图6.6摄氏度)是真实的或纯粹的产品抽样可变性。整流罩et al。(1996)设计了引导算法构造一个信心乐队在(T);一个是显示为算法6.1。
步骤2的算法,离散化(T)使用了一个很大的数,,几百名的顺序,呈现平滑估计。第四步,选择引导方法,还模拟集是一个随机变量的大小,测试了整流罩et al . (1996)。Studentiza-tion(步骤8)吸引优势,辅助变量Tstud (T, b)大约是关键(T)独立的替代词
1000年
1200年
1400年1600年
1800年
图6.6。易北河冬季洪水、带宽选择、沉重的事件(大小2 - 3)。出现率估计与pseudodata(“两点”规则)和带宽h = 5(一个),100 (b)和35 (c)。
1000年
1200年
1400年1600年
1800年
2000年
图6.6。易北河冬季洪水、带宽选择、沉重的事件(大小2 - 3)。出现率估计与pseudodata(“两点”规则)和带宽h = 5(一个),100 (b)和35 (c)。
施工方法(百分比)这一步测试整流罩et al。(1996)。由此产生的信心乐队(步骤12)是一个点态。
的覆盖性能信心乐队(算法6.1)测试通过蒙特卡罗模拟(整流罩1995;整流罩et al . 1996;大厅2008页,个人沟通)。规定(T)功能有正弦信号的形式添加到一个线性趋势。非单调曲线类似于气候可能会发现(图6.6摄氏度)。raybet雷竞技最新这使得在这本书的上下文中相关的实验。极端数据的数量,j,几百的顺序。蒙特卡罗方法的结果显示良好的覆盖性能(6.1算法),并选择的重采样或CI建设。
步骤1事件,增强了pseudodata (Eq。6.34)第二步离散化的时间T
步骤3 (Nt)内核发生速度估计(Eq。6.33)第四步从数据集(步骤1),与更换一组模拟的大小m)第5步内核发生速率估计,模拟数据,利用h一样在第6步步骤3到步骤4直到b = b(通常是b = 2000)复制存在第7步平均步骤8 Studentize第9步确定助教低10步CI绑定在T第11步上CI绑定在T步骤12信心乐队是由联合CIs / T
(T) = b - 1£f = 1 A * b (T)
Tstud (T, b) = (A * b (T) - (T)) (A * b (T)) - v2
# {| Tstud (T, b) | < ta} =(1 - 2)“挪威通讯社”星期六报导
算法6.1。建设引导信心区间内核发生速度估计(整流罩et al . 1996年)。(第9步需要插值由于病例数,#,是离散的)。CI类型叫做percentile-t。
6.3.2.7例子:冬天易北河洪水(继续)
图6.7显示了沉重的冬天易北河的出现率和90%置信区间洪水。很长的增加从年最终以一个高的开始在16世纪下半叶,(T) 0.17 w A - 1时,对应的重现期6年。更改一个低在1700左右(0.08 w (T) a - 1)和随后的高上半年的十九世纪(0.22 w (T) a - 1)是重要的,带证明的信心。上层CI开往高大约0.31是一流的。易北河冬季洪水风险下降,这种趋势一直持续到现在。
T ro
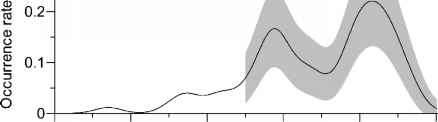
图6.7。易北河冬季洪水、出现率估计,沉重的事件(大小2 - 3)。带阴影的信心。估计参数在图6.6 c: pseudodata生成规则“两点,”h = 35;元= 1322,B = 2000;置信水平:1 - 2 = 90%。
1000 1200 1400 1600 1800 2000
一年
图6.7。易北河冬季洪水、出现率估计,沉重的事件(大小2 - 3)。带阴影的信心。估计参数在图6.6 c: pseudodata生成规则“两点,”h = 35;元= 1322,B = 2000;置信水平:1 - 2 = 90%。
在一份简短的解释数学发现,长期增加的结果数据不均匀性文档的形式损失。很可能从欧洲印刷术的发明之前的文件中(15世纪)不是很多,和过去的信息洪水可能已经失去了之前找到进入二次编译。因此信心乐队只间隔公元后。1500。16世纪末据说湿也在欧洲中部和西南部的其他部分(Brazdil et al . 1999年)。洪水风险相对较低在T = 1700年可能是一个干燥的表现(冷)欧洲气候(Luterbacher et al . 2001年)末的蒙德极小期(图2.12)。raybet雷竞技最新T w 1830年到现在的下降趋势反映了一种冰洪水的风险(如,在减少
1784),反过来是一个产品的表面易北河地区的气候变暖(2004年Mudelsee et al . 2003年)。
6.3.2.8例子:火山山峰在硫酸NGRIP记录(继续)
图6.8显示了一个数量的高点和低点出现极端NGRIP冰芯记录中硫酸盐的山峰从~ 10 ~ 110 ka。应用更加自由的检测阈值(z = 5.0)会导致更多的事件,相对误差较小(rc m i / 2)和更高的意义(T)的变化,但也更为保守的阈值(z = 10.0)的变化表现为显著。估计接近观察区间的边界取决于pseudodata生成规则(没有显示),应谨慎解释。
“超额”建设硫酸记录(图1.4)和极端检测(图4.16)中提取的目的从冰芯记录的信息主要的火山喷发发生。对于带宽选择,我们忽略交叉验证和设置h = 5 ka能够检查火山活动在米兰柯维奇时间尺度的变化(^ 19 ka)。尘封气候变化这样raybet雷竞技最新的轨道时间尺度(第五章),并研究火山活动和尘封气候之间的因果关系是促进通过常见的动力。看到背景材料(6.5节)。
6.3.2.9例子:飓风山峰下神秘湖纹泥厚度记录(继续)
图6.9显示了飓风在波士顿地区的出现率(降低神秘湖)。带宽选择征收轻微un-dersmoothing (h = 50);进一步undersmoothing会产生太多无意义的摆动。有更高的飓风活动在十三世纪;90%可信区间的上限接近每十年一个事件。飓风活动后,也有可能,那个时期较低。Cox-Lewis测试(6.3.2.10节)一个总体趋势是不确定的(u = -1.15, p = 0.12),由于非风险曲线和有限的样本大小。
气候的解释可能会注意到一个高在飓风活动之间的关系中世纪暖期。飓风的风险升高,因此可能是由于卡诺机在大西洋热带地区(1987年伊曼纽尔,1999),由于更高的海洋表面温度在此期间(1996年齐格纹)。然而,Besonen et al。(2008:第四节在其中)承认“这LML(较低的神秘湖)记录单个点源记录代表大波士顿地区
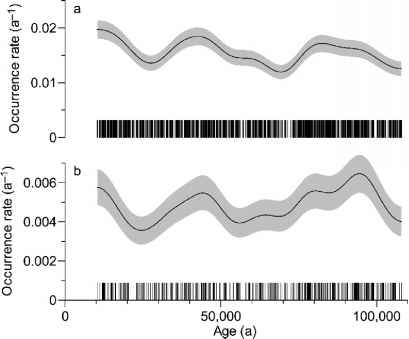
图6.8。硫酸NGRIP记录,火山活动的评估。硫酸极端源于火山喷发被发现(图4.16)通过应用阈值z = 5.0 (a)和z = 10.0 (b)和declustering。活动时间(m = 1525;b m = 475)显示为酒吧、出现率为实线,带阴影的信心。评估参数:pseudodata生成规则“反射”,h = 5000;元= 574,B = 2000;置信水平:1 - 2 = 90%。
图6.8。硫酸NGRIP记录,火山活动的评估。硫酸极端源于火山喷发被发现(图4.16)通过应用阈值z = 5.0 (a)和z = 10.0 (b)和declustering。活动时间(m = 1525;b m = 475)显示为酒吧、出现率为实线,带阴影的信心。评估参数:pseudodata生成规则“反射”,h = 5000;元= 574,B = 2000;置信水平:1 - 2 = 90%。
和飓风经过几百公里的东或西可能没有产生很重的降雨量和植被扰动在湖里分水岭必要LML沉积物中产生一个强烈的信号。”
6.3.2.10参数泊松模型和假设测试
可以制定一个参数回归模型(第4章)出现率。自(T)不能是负数,方便采用指数函数。一个特别简单的模型
(T) = exp (Ao +)。(6.39)另一个是物流模型,exp (Ao +人工智能T)
(T) = 1 + exp (Ao + AiT)。(640)
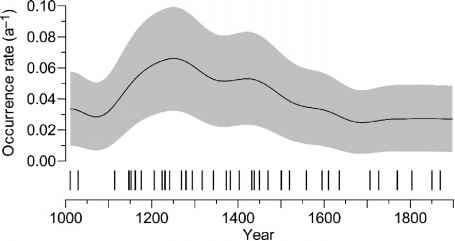
图6.9。低神秘湖纹泥厚度记录,飓风活动评估。飓风事件检测(图4.17)通过应用一个阈值z = 5.2和实施第二个条件(分级床)。活动时间(m = 36)显示为酒吧、出现率为实线,带阴影的信心。评估参数:pseudodata生成规则“反射”,h = 50;元= 616,B = 2000;置信水平:1 2 = 90%。
图6.9。低神秘湖纹泥厚度记录,飓风活动评估。飓风事件检测(图4.17)通过应用一个阈值z = 5.2和实施第二个条件(分级床)。活动时间(m = 36)显示为酒吧、出现率为实线,带阴影的信心。评估参数:pseudodata生成规则“反射”,h = 50;元= 616,B = 2000;置信水平:1 2 = 90%。
这两个是单调函数,它们可以用来模拟简单的增加(减少)的发生率。6.5节列出更多的参数出现率模型。这些模型没有提供非参数核方法的灵活性(6.3.2.2节)。参数化模型更适合情况的任务没有量化(T),而是测试(T)是否显示了增加(减少)。考克斯和刘易斯(1966)使用简单的模型(Eq。6.39)来测试假设H1: > 0”(出现率增加)对总部= 0”(常数出现率)。他们的检验统计量
并且随着m,迅速成为标准正态分布形状(克莱默1946:p。245在其中)。在样本层次,插入{t0ut (j)}”1, t(1)(观测时间间隔,开始)和t (n)(观测时间间隔,结束)获得u。
6.3.2.11蒙特卡洛实验:Cox-Lewis测试与Mann-Kendall测试
Cox-Lewis统计(Eq。6.41)可以用来测试单调趋势的发生极端,Mann-Kendall统计(Eq。4.61)是测试开发的变化Xtrend (T)的这个理论不适合Mann-Kendall测试(Zhang et al . 2004年),然而,并不是阻碍气候学家和水文学家应用研究极端。
我们分析的性能测试与气候现实蒙特卡罗实验数据生成过程的属性:持续噪声组件具有非正态分布形状和局外人或极端的组件,展品发生率的上升趋势。这意味着,我们研究整个过程的性能,采用在实践:检测极端和检测发生的趋势。

图6.10。密度函数用于蒙特卡罗试验(表6.1,6.2,6.3和6.4)。噪音的PDF组件(实线)是一个对数正态,极端的PDF组件(取代了噪声组件在一个极端的发生)是卡方分布与v = 1自由度和转移重定向的值为1.0 (short-dashed线)和3.0 (long-dashed线),分别。
图6.10。密度函数用于蒙特卡罗试验(表6.1,6.2,6.3和6.4)。噪音的PDF组件(实线)是一个对数正态,极端的PDF组件(取代了噪声组件在一个极端的发生)是卡方分布与v = 1自由度和转移重定向的值为1.0 (short-dashed线)和3.0 (long-dashed线),分别。
图6.10显示了在一个仿真环境(1.0)离群值组件转移异常值和噪声组件的pdf重叠一个好的学位,而在另一个(3.0)将pdf文档仅重叠强烈程度降低。
表6.1。蒙特卡洛实验中,假设测试的趋势发生的极端。nsim = 90000随机样本来自X (i) = Xout(我)+ Xnoise (i), T (i) =我的地方,我= 1,……,n和噪声是一个AR(1)过程= 1 / e ~ 0.37,对数正态形状,平均和标准偏差1.0 0.5(表3.5)。极端的数量,mtrue规定。极端事件,兜售(j),通过一个随机变量生成均匀分布在[0;1]的k和它线性映射(T (1);T (n)];参数k开出出现率的趋势。Xout (j)是来自一个移位(x + 1)卡方分布与v = 1; this extreme value replaced the value Xnoise(i) for which the time, T(i), was closest to Tout (j). Extremes detection employed a constant threshold of median + 3.5 MAD (Fig. 4.15) for the POT approach and a block length of k = 12 (Fig. 6.2) for the block extremes approach. The Cox-Lewis test was applied to the detected POT data, the Mann-Kendall test to the POT data and also the block extremes. The significance level of the one-sided tests was a = 0.10.
n |
mtrue |
Kb |
实证powerc |
||
测试 |
|||||
Cox-Lewis |
Mann-Kendall |
Mann-Kendall |
|||
(罐) |
极端(块) |
(罐) |
|||
120年 |
10 |
0.75 |
0.161 |
0.089 |
0.041 |
240年 |
20. |
0.75 |
0.181 |
0.099 |
0.069 |
600年 |
50 |
0.75 |
0.236 |
0.150 |
0.077 |
1200年 |
One hundred. |
0.75 |
0.313 |
0.217 |
0.096 |
2400年 |
200年 |
0.75 |
0.434 |
0.338 |
0.125 |
6000年 |
500年 |
0.75 |
0.680 |
0.619 |
0.194 |
12000年 |
1000年 |
0.75 |
0.883 |
0.868 |
0.300 |
120年 |
10 |
0.9 |
0.129 |
0.065 |
0.036 |
240年 |
20. |
0.9 |
0.132 |
0.066 |
0.058 |
600年 |
50 |
0.9 |
0.147 |
0.080 |
0.059 |
1200年 |
One hundred. |
0.9 |
0.166 |
0.093 |
0.065 |
2400年 |
200年 |
0.9 |
0.195 |
0.115 |
0.073 |
6000年 |
500年 |
0.9 |
0.268 |
0.176 |
0.089 |
12000年 |
1000年 |
0.9 |
0.357 |
0.261 |
0.109 |
一个真正的(规定的)数量的极端。
b规定发生率趋势参数,(T) < x T 1 / k - 1。
c的模拟Ho的地方:“没有趋势”拒绝对H1:“向上的趋势,”除以nsim。标准误差(埃夫隆和Tibshirani 1993)名义上[(1 - 1)/ nsim] 1/2 = 0.001。
一个真正的(规定的)数量的极端。
b规定发生率趋势参数,(T) < x T 1 / k - 1。
c的模拟Ho的地方:“没有趋势”拒绝对H1:“向上的趋势,”除以nsim。标准误差(埃夫隆和Tibshirani 1993)名义上[(1 - 1)/ nsim] 1/2 = 0.001。
结果(表6.1,6.2,6.3和6.4)可以概括如下。
1。高数量的极端允许更好的检测能力(T)的趋势。
表6.2。蒙特卡洛实验中,假设测试的趋势发生极端的(持续)。模拟的数量在每种情况下nsim = 47500。片面的显著性水平测试是一个= 0.05。改变参数的异常值组件是1.0。详情见表6.1。
表6.2。蒙特卡洛实验中,假设测试的趋势发生极端的(持续)。模拟的数量在每种情况下nsim = 47500。片面的显著性水平测试是一个= 0.05。改变参数的异常值组件是1.0。详情见表6.1。
n |
mtrue |
Kb |
实证powerc |
||
测试 |
|||||
Cox-Lewis |
Mann-Kendall |
Mann-Kendall |
|||
(罐) |
极端(块) |
(罐) |
|||
120年 |
10 |
0.75 |
0.085 |
0.043 |
0.020 |
240年 |
20. |
0.75 |
0.101 |
0.058 |
0.029 |
600年 |
50 |
0.75 |
0.139 |
0.092 |
0.040 |
1200年 |
One hundred. |
0.75 |
0.195 |
0.142 |
0.051 |
2400年 |
200年 |
0.75 |
0.297 |
0.238 |
0.070 |
6000年 |
500年 |
0.75 |
0.542 |
0.494 |
0.120 |
12000年 |
1000年 |
0.75 |
0.797 |
0.785 |
0.200 |
120年 |
10 |
0.9 |
0.065 |
0.030 |
0.018 |
240年 |
20. |
0.9 |
0.069 |
0.035 |
0.026 |
600年 |
50 |
0.9 |
0.079 |
0.044 |
0.029 |
1200年 |
One hundred. |
0.9 |
0.089 |
0.052 |
0.033 |
2400年 |
200年 |
0.9 |
0.雷竞技csgo111 |
0.069 |
0.038 |
6000年 |
500年 |
0.9 |
0.166 |
0.108 |
0.049 |
12000年 |
1000年 |
0.9 |
0.234 |
0.173 |
0.061 |
一个真正的(规定的)数量的极端。
b规定发生率趋势参数,(T) < x T 1 / k - 1。
c的模拟Ho的地方:“没有趋势”拒绝对你好:“向上的趋势,”除以nsim。标准错误是名义上[(1 - 1)/ nsim] i / 2 = 0.001。
一个真正的(规定的)数量的极端。
b规定发生率趋势参数,(T) < x T 1 / k - 1。
c的模拟Ho的地方:“没有趋势”拒绝对你好:“向上的趋势,”除以nsim。标准错误是名义上[(1 - 1)/ nsim] i / 2 = 0.001。
2。给极端较大值(位移参数)提高检测能力和检测趋势的力量(T)。
3所示。执行一个测试在一个较低的显著性水平(a)减少了权力(如一般假设测试)。
4所示。更强的趋势(T)(参数k)可以更容易检测到(更高的权力)。
5。所有设置的最佳性能,研究,实现了Cox-Lewis测试。例如,当数据大小n = 1200,变化参数为3.0,规定数量的极端mtrue = 100,相当于平均(T)的1/12,和k = 0.75,这意味着增加(T)«T (。333,那么这种向上趋势可以检测到Cox-Lewis测试在大约10%的水平所有病例的84.2%(表6.3)。
表6.3。蒙特卡洛实验中,假设测试的趋势发生极端的(持续)。模拟的数量在每种情况下nsim = 90000。片面的显著性水平测试是一个= 0.10。改变参数的异常值组件是3.0。详情见表6.1。
表6.3。蒙特卡洛实验中,假设测试的趋势发生极端的(持续)。模拟的数量在每种情况下nsim = 90000。片面的显著性水平测试是一个= 0.10。改变参数的异常值组件是3.0。详情见表6.1。
n |
mtrue |
Kb |
实证powerc |
||
测试 |
|||||
Cox-Lewis |
Mann-Kendall |
Mann-Kendall |
|||
(罐) |
(blocfc极端) |
(罐) |
|||
120年 |
10 |
0.75 |
0.267 |
0.145 |
0.064 |
240年 |
20. |
0.75 |
0.377 |
0.200 |
0.069 |
600年 |
50 |
0.75 |
0.622 |
0.379 |
0.080 |
1200年 |
One hundred. |
0.75 |
0.842 |
0.603 |
0.098 |
2400年 |
200年 |
0.75 |
0.977 |
0.857 |
0.125 |
6000年 |
500年 |
0.75 |
1.000 |
0.996 |
0.188 |
12000年 |
1000年 |
0.75 |
1.000 |
1.000 |
0.280 |
120年 |
10 |
0.9 |
0.143 |
0.080 |
0.056 |
240年 |
20. |
0.9 |
0.169 |
0.088 |
0.057 |
600年 |
50 |
0.9 |
0.229 |
0.122 |
0.062 |
1200年 |
One hundred. |
0.9 |
0.308 |
0.167 |
0.065 |
2400年 |
200年 |
0.9 |
0.442 |
0.246 |
0.070 |
6000年 |
500年 |
0.9 |
0.709 |
0.450 |
0.089 |
12000年 |
1000年 |
0.9 |
0.909 |
0.696 |
0.106 |
一个真正的(规定的)数量的极端。
b规定发生率趋势参数,(T) < x T 1 / k-l。
c的模拟Ho的地方:“没有趋势”拒绝对你好:“向上的趋势,”除以nsim。标准错误是名义上[(1 - 1)/ nsim] l / 2 = 0.001。
一个真正的(规定的)数量的极端。
b规定发生率趋势参数,(T) < x T 1 / k-l。
c的模拟Ho的地方:“没有趋势”拒绝对你好:“向上的趋势,”除以nsim。标准错误是名义上[(1 - 1)/ nsim] l / 2 = 0.001。
6。Mann-Kendall测试可能应用于极端数据块,{兜售(j), Xout (j)} j =我,在中央的一块作为宣传(j)。这导致功率水平在实践中可能是可以接受的。然而,在所有模拟设置Cox-Lewis测试表现明显优于Mann-Kendall测试。(注意,块长度的调优,k,导致m = mtrue。这可能提高测试能力相比情况k调整。)
7所示。Mann-Kendall测试应用于数据会导致一个不够格的测试能力。
因此,我们推荐使用Cox-Lewis测试而不是任何形式的Mann-Kendall测试为研究趋势在极端事件的发生。
表6.4。蒙特卡洛实验中,假设测试的趋势发生极端的(持续)。模拟的数量在每种情况下nsim = 47500。片面的显著性水平测试是一个= 0.05。改变参数的异常值组件是3.0。详情见表6.1。
表6.4。蒙特卡洛实验中,假设测试的趋势发生极端的(持续)。模拟的数量在每种情况下nsim = 47500。片面的显著性水平测试是一个= 0.05。改变参数的异常值组件是3.0。详情见表6.1。
n |
mtrue |
Kb |
实证powerc |
||
测试 |
|||||
Cox-Lewis |
Mann-Kendall |
Mann-Kendall |
|||
(罐) |
极端(块) |
(罐) |
|||
120年 |
10 |
0.75 |
0.154 |
0.072 |
0.028 |
240年 |
20. |
0.75 |
0.240 |
0.116 |
0.035 |
600年 |
50 |
0.75 |
0.465 |
0.262 |
0.043 |
1200年 |
One hundred. |
0.75 |
0.728 |
0.474 |
0.055 |
2400年 |
200年 |
0.75 |
0.944 |
0.771 |
0.072 |
6000年 |
500年 |
0.75 |
1.000 |
0.991 |
0.117 |
12000年 |
1000年 |
0.75 |
1.000 |
1.000 |
0.185 |
120年 |
10 |
0.9 |
0.073 |
0.036 |
0.025 |
240年 |
20. |
0.9 |
0.090 |
0.046 |
0.028 |
600年 |
50 |
0.9 |
0.128 |
0.068 |
0.031 |
1200年 |
One hundred. |
0.9 |
0.188 |
0.099 |
0.034 |
2400年 |
200年 |
0.9 |
0.298 |
0.157 |
0.037 |
6000年 |
500年 |
0.9 |
0.567 |
0.329 |
0.048 |
12000年 |
1000年 |
0.9 |
0.831 |
0.577 |
0.060 |
一个真正的(规定的)数量的极端。
b规定发生率趋势参数,(T) < x T 1 / k-l。
c的模拟Ho的地方:“没有趋势”拒绝对你好:“向上的趋势,”除以nsim。标准错误是名义上(1 - 1)/«,sim) l / 2 = 0.001。
一个真正的(规定的)数量的极端。
b规定发生率趋势参数,(T) < x T 1 / k-l。
c的模拟Ho的地方:“没有趋势”拒绝对你好:“向上的趋势,”除以nsim。标准错误是名义上(1 - 1)/«,sim) l / 2 = 0.001。
继续阅读:马dfCOV dTA 1 x M
这篇文章有用吗?