重力波

周期性运动的两个类的概述,重力波是最研究内河和最好的理解。我们将只考虑线性波,振幅的振荡运动温跃层是小的比表面和底部层的深度。这不是一个主要的限制分析,包含的非线性效应已被证明在大多数情况下,只需要一个小小的修正线性近似。在本文中,我们关注的情况下汉堡号码是~ 1,这样旋转效应可以预期。对表面波(正压),这通常需要超过300公里宽的湖泊,很少有。斜压动作,相速度c是远远低于正压动作,有许多湖泊,汉堡号码是~ 1。典型的斜压值内部波相速度(0.05 - -0.4 ms-1),内部罗斯比~ 1 - 5公里半径(图1),表明内部重力波在湖泊的规模(或更大)应该体验地球的旋转效应。还要注意与正压阶段的速度不同,这取决于水深,斜压阶段速度变化的函数分层,因此通过改变。旋转可能因此扮演更重要的角色在内部波动力强烈分层期间当内部罗斯比半径(因此汉堡数量)比在其他时间最小。

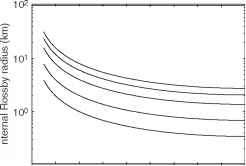
c = 0.4 m / s c = 0.3 m / s c = 0.2 m / s c = 0.1 m / s c = 0.05 m / s

0 10 20 30 40 50 60 70 80 90纬度

图1内部罗斯比半径作为纬度数的函数内部波速度。水平长度尺度相似或大于内部罗斯比半径、旋转的影响应该被观察到。

c = 0.4 m / s c = 0.3 m / s c = 0.2 m / s c = 0.1 m / s c = 0.05 m / s

0 10 20 30 40 50 60 70 80 90纬度

图1内部罗斯比半径作为纬度数的函数内部波速度。水平长度尺度相似或大于内部罗斯比半径、旋转的影响应该被观察到。

理解这些动作的形式在内陆水域,建立我们的知识是很有意义的简单的系统。我们开始在一个没有边界的旋转系统,比如在海洋中间远离海岸,在经典的重力波的解决方案被称为平面进步庞加莱波。振幅(q)和速度结构(u, v)与这些波可以被描述为q - q0 cos (kx -在)

u是速度在波的传播方向,v是速度在横向方向上,q0最大振幅,k是波数(2 p / l, l是波长),一个是波频率(2 p / T, T波的周期),H是水深(或等效水深他内部波),f是惯性频率。流体粒子轨迹(在计划视图中,垂直运动很小由于线性波的假设)与大轴椭圆的方向传播,与椭圆轴之比等于a / f和旋转的方向anticy-clonic(即。地球的旋转方向相反,)。简称波,高频,a / f是大所以轨迹椭圆细长。长波浪相反,a / f接近一波频率低,因此粒子轨道是圆形的,描绘出海洋中著名的“惯性圈”(图2)。这些圆形轨道的半径是U / f,可以使用命令新配方。[11]和[12]q0 / kH。

内波的动力学的一个重要方面受到地球自转的影响,能量通常是不同样的分离动力学和潜在形式。平面的进步波庞加莱(图2),单位面积上的平均动能

其中p是水的密度,单位面积上的势能

这样的比率可能是动能

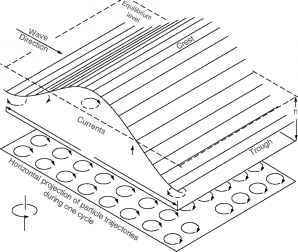
图2很长的飞机进步庞加莱波,在无限的海洋,A ~ f。注意电流向量的旋转是地球自转的方向相反。从莫蒂默复制CH(1974)湖泊水动力学。手套。Int,版本。定理。Angew。Limnol。20: 124 - 197 e . Schweizerbart(许可http://www.schweizerbart.de/)。

图2很长的飞机进步庞加莱波,在无限的海洋,A ~ f。注意电流向量的旋转是地球自转的方向相反。从莫蒂默复制CH(1974)湖泊水动力学。手套。Int,版本。定理。Angew。Limnol。20: 124 - 197 e . Schweizerbart(许可http://www.schweizerbart.de/)。

动能比接近一个(如不旋转情况下f ! 0),和波接近惯性频率接近于零势能信号(如波如图2所示)。这对测量这些电波,他们通常只会被观察到的电流测量(测量的动能)而不是波动分层(衡量势能变化)。

引入边界允许存在的开尔文波。经典的开尔文波的解决方案是一个速度垂直于岸边被认为是零(图3)。这些电波传播平行于边界的最大振幅在岸边,在海浪波峰向右(在北半球)沿着传播方向时。振幅降低离岸速度等于指数罗斯比半径变形R, q - q0e y /有数(kx -在)

这表明波的频率大于惯性频率将有潜力

其中x是近岸方向和传播方向,y是离岸方向(图3)。请注意,波的相速度是c = y / gH,一样一波在不旋转系统中。电流向量,根据定义,是直线和近岸方向的振动。与波在不旋转坐标系,潜在的动能是统一的比率。内部开尔文波的动力学是相同的,除了斜压阶段速度适用和波振幅降低

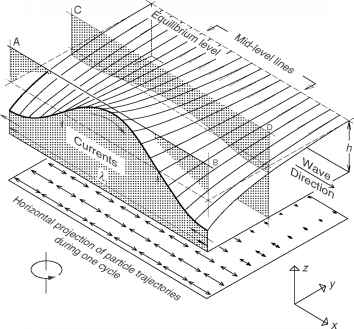
图3开尔文波x-positive方向发展,海岸位于y = 0。垂直通道的墙壁可以放置在任意点的y,例如飞机AB和CD所示。从莫蒂默复制CH(1974)湖泊水动力学。手套。Int,版本。定理。Angew。Limnol。20: 124 - 197,与许可•••(http://www.schweizerbart.de/)。

图3开尔文波x-positive方向发展,海岸位于y = 0。垂直通道的墙壁可以放置在任意点的y,例如飞机AB和CD所示。从莫蒂默复制CH(1974)湖泊水动力学。手套。Int,版本。定理。Angew。Limnol。20: 124 - 197,与许可•••(http://www.schweizerbart.de/)。

指数离岸与内部罗斯比半径变形Ri。

第二个边界的引入大大复杂化海浪在旋转系统的支持。通道(定义为两个平行墙张开结束)能够支持进步庞加莱波,由斜进步庞加莱入射波的反射,和站在庞加莱电波,由两个相反的方向进步庞加莱波浪。这些波由细胞类似图2和图3中给出,不过速度在每个单元的边界趋于零。关闭一个盆地,因此创建一个“湖”明显复杂波场。矩形盆地,由于复杂的角落,一个事件+一个反映开尔文波是必需的和无限的庞加莱相同的声波频率满足边界条件。可以找到更简单的解决方案假设湖泊是由圆形或椭圆盆地的统一的深度,我们将在下面讨论。正如前面介绍的,一个关键的无量纲参数控制这个响应美国的汉堡号码是根据这个参数,可以确定波频率为圆形和椭圆形盆地,势能,动能的比值在波响应,和盆地外部强迫的响应。我们还将依赖于简化开尔文和飞机进步庞加莱波前面描述协助解释结果。

了解波的空间结构(和他们引起的电流)在旋转系统中,它是有用的考虑两个端点:强烈的旋转(S ! 0)和不旋转(Sn)。对于内陆水域,这些也可能被认为是“大湖”和“小湖的情况下。S ^ 0,在内地的湖,我们可能期望飞机进步庞加莱波出现正如前面列出的(图2),频率方法惯性频率,电流矢量旋转anticyclonically和大部分的能源动力形式。在湖边边界,我们可能期望古典开尔文波的解决方案,在离岸衰变振幅指数R,速度速度边界平行于岸边,势能,动能的比例是统一和频率趋于0(图3)。从北方收集的数据美国的五大湖支持这一概念模型,与室内的运动由near-inertial频率和运动边界的形式出现在“沿海飞机”的表现开尔文波的解决方案。随着变小(即湖。为Sn),我们应该期待波,类似于不旋转的情况下,潜在的动能是统一的比率,和离岸衰变振幅不再是指数,和当前向量成为直线(即。,椭圆变得细长)。

这些波的特征如何变化的函数汉堡的数量和长宽比湖是图形如图4所示。nondi-mensional频率o / f和潜力提出了动能的比值分析解决圆形和椭圆盆地为气旋(Kelvin-type)和反气旋(Poincare-type)波。注意潜在的动能比率是集成在整个湖,不代表人物在特定点在空间。我们首先考虑波在一个圆形盆地(方面

0

0.6 0.4 0.2 0

汉堡(R / L)数量

汉堡(R / L)数量

- e -	气旋(1:1)
- - - - - - -	气旋(2:3)
■■□■	气旋(1:3)
- * -	Anti-cyclonic(1:1)
- v -Anti-cyclonic(2:3)
0	Anti-cyclonic (1:3)

图4无量纲频率(上半部分)和潜在的比动能(下图)作为波函数类型和比例,括号里的数字表示的长宽比。无量纲频率的绝对值作为半球的结果是独立的。复制从Antenucci JP Imberger J(2001)能量的内部重力波在大湖。湖沼学和海洋学46:1760 - 1773,美国社会的许可湖沼学和海洋学。

图4无量纲频率(上半部分)和潜在的比动能(下图)作为波函数类型和比例,括号里的数字表示的长宽比。无量纲频率的绝对值作为半球的结果是独立的。复制从Antenucci JP Imberger J(2001)能量的内部重力波在大湖。湖沼学和海洋学46:1760 - 1773,美国社会的许可湖沼学和海洋学。

由定义是1:1比例)。在强烈的旋转情况下(S ! 0),气旋波频率趋于零,能量比方法统一。这是半无限边界的开尔文波限制了早些时候(图3)。反气旋波,频率方法惯性频率和主要是动能——飞机进步庞加莱波解决方案(图2)早些时候了。随着年代的增加,两种类型的波的波频率增加,慢慢收敛湖变小。反气旋波的能量比也增加和渐近方法统一,nonrotation限制(Sn)。气旋波的能量比率增加到最多~ 1.5,在渐近接近团结Sn。重要的是Sn这两个解决方案具有相同的特性(频率、能量比cross-basin结构),除了他们在相反的方向旋转。他们会因此表现在高年代驻波。

潜在的分布(即。(即,温跃层振荡)和动能。,电流)盆地也改变旋转变化(图5)的重要性。对于强烈旋转的情况(S ! 0), cross-shore势能气旋波的结构相关的指数衰减开尔文波传播沿着海岸线,我们可以重写eqn。[14]q = q0e ~ 3 = SL这小S指数衰减迅速相对于湖宽度(图5 (a))。动能也主要是靠近岸边(图5 (c)),因此“沿海飞机”这个词被应用到这些运动在北美五大湖。旋转的重要性减少(增加),有一个强大的气旋波出现在内部的信号。重要的是要注意,对于这种情况,电流不平行于边界在旁边的湖——海岸线他们保持平行,如图3;然而,向室内,当前椭圆越来越圆,实际上在气旋旋转方向。反气旋(Poincare-type)波的结构变化非常小的重要性旋转变化(图5 (b)和5 (d))。请注意,Sn、势能和动能的分布在气旋波反气旋波的方法。

我们现在考虑的影响改变长宽比由一个圆形向椭圆盆地盆地形状。注意罗斯比半径椭圆盆地定义基于长轴的长度,短轴,如图4所示。减少宽高比的影响是不旋转情况下的系统的方法降低美国的价值观与圆形盆地,的频率

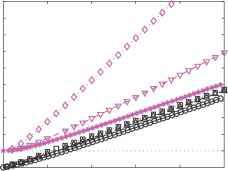
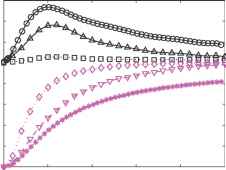
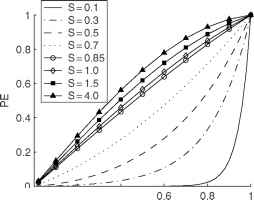
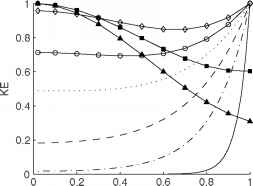
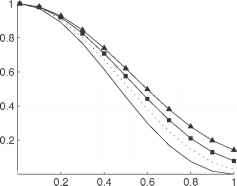
图5的径向结构气旋和反气旋波能量分布的函数汉堡数量为一个圆形湖最低频率运动(基本模式)。气旋波结构所示面板(a)和(c),反气旋波结构所示面板(b)和(d)。每个汉堡的径向结构已经被其最大值归一化。请注意,并不是所有的汉堡数字所示面板(b)和(d)。注意的指数衰减(a)是一样的,在图3中,eqn表示。[16]。复制从Antenucci JP Imberger J(2001)能量的内部重力波在大湖。湖沼学和海洋学46:1760 - 1773,美国社会的许可湖沼学和海洋学。

每一对气旋和反气旋波发散而不是收敛。在Sn的极限,气旋波转变成纵向湖面,而反气旋波成为横向假潮的解决方案。正是因为这一原因,风力在横向方向上已经观察到更容易产生反气旋,Poincare-type,波。

继续阅读:Txz PK和tyz PK

这篇文章有用吗?

0 0