部分吸收大气
支撑黑体的假设辐射公式辐射与物质的相互作用如此强烈以至于在与物质相同的温度下达到热力学平衡。因此,如果一盒气体中含有的分子太少,无法提供足够的机会来拦截光子,那么发射就会偏离黑体定律。与辐射的弱相互作用也可能产生于抑制相互作用的材料结构方面,如食盐或二氧化碳冰的晶体结构。在任何一种情况下,发射率对普朗克分布的偏离都是由发射率来表征的。假设I(v, n)是观测到的频率为v的从一个物体向n方向发出的辐射通量。则发射率e(v, n)由表达式定义
T是我们观测到的物质集合的温度。请注意,在给物体指定温度T时,我们假设物质本身处于热力学平衡状态。发射率也可能是温度和压力的函数。我们还可以定义频率上的平均发射率,以及从物体发出的所有射线。平均发射率是f n e(v, n)B(v, T) cos OdvdQ
其中0是射线与物体表面法线的夹角角积分是在射线离开物体表面的半球上进行的。根据这个定义,从物体表面的任何一块区域产生的净通量为F = e-T4。即使e不显式地依赖于温度,如果e依赖于频率,e也将依赖于温度,因为由B(v, T)决定的不同频率的相对权重随温度而变化。
黑体在所有频率和方向上都有单位发射率。黑体也有单位吸收率,这只是黑体与辐射场强烈相互作用的一种情况的重申。对于一个非黑体,我们可以定义吸收率a(v, n),方法是用给定频率和方向的光照射物体,测量有多少被反射,有多少从另一侧出来。具体来说,假设我们发射一束电磁能量方向n,频率v,通量Finc在测试对象上。然后,我们测量一旦光束打开,物体发出的额外能量通量。由于入射光束的散射,这种向外的通量可以从许多不同的方向出来;在特殊情况下,甚至频率也可能不同于入射辐射.设T和R为透射和反射能量通量,对所有角度和频率积分。然后,吸收率通过取留在体内的能量通量与入射通量的比率来定义。因此,
/ Finc -(T + R) / " 00n a(v, n) =——(3.22)
普朗克函数无疑是定义具有温度t的物体的平均发射率ee的加权函数的自然选择,但在所有频率和方向上定义平均吸收率没有这样独特的选择。适当的加权函数是由入射辐射的频率和方向谱决定的,这需要对其来源有详细的了解。如果入射辐射是一个温度为Tsource的黑体,则a应按公式如式3.20定义,使用B(v, Tsource)作为加权函数。注意,加权函数是由源的温度定义的,而不是由吸收物体的温度定义的。与平均发射率的情况一样,加权函数的温度依赖性意味着即使a = a(v), a也将随Tsource而变化,并且不明显依赖于温度。
吸收率和发射率似乎是一个物体的独立特征,但观察和理论论证揭示了两者之间的密切关系。基尔霍夫辐射定律所表达的这种关系是辐射与物质相互作用的深刻性质,是所有辐射转移理论的核心。基尔霍夫定律指出,物质在任何给定频率下的发射率等于在同一频率下测量的吸收率。它最初是通过实验推断出来的。19世纪晚期勤奋的光谱学家利用他们的新技术测量了各种物体在不同温度下的发射光谱I(v, n, T)和吸收率a(v, n, T)。基尔霍夫发现,除了少数发光材料的发射与温度无关外,一旦观测到的发射被观测到的吸收率归一化,所有的实验数据都坍塌到一条单一的通用曲线上,与材料无关。换句话说,几乎所有材料符合我的关系(v、n T) / (n v, T) = f (v, T)相同的函数f。如果我们把一个完美的吸收器的极限——一个完美的“黑色”的身体,那么f = 1,我们发现,事实上我们已经调用普朗克函数B (v, T)。事实上,正是这种外推到一个完美的减震器,最初制定了黑体辐射的概念。由于f = B和I = eB,我们恢复了e/a = 1形式的基尔霍夫定律的表述。
图3.12所示的思想实验允许我们从热力学第二定律的要求推导出平均吸收率和发射率的基尔霍夫定律。我们考虑温度为的两个无限大的黑体材料板,它们之间有一个间隙。在缝隙中,我们引入一块部分透明的材料板,其平均吸收率a(Ti)和平均发射率e(T1),其中T1是测试材料的温度。注意,这个系统是能量封闭的。接下来,我们要求黑体材料和测试对象之间的辐射传递导致系统向等温状态演化。换句话说,我们假设辐射热传递满足第二定律。辐射传递迫使系统向等温状态演化的必要条件是等温状态to = T1是系统的平衡状态;如果不是最初的等温状态就会自发地产生温度不均匀性。能量平衡要求2a(To)aT4 = 2e(T1)aT-j4。基尔霍夫定律紧随其后,在能量平衡中设置To = T1,这意味着a(To) = e(To)。 Note that the mean absorptivity in this statement is defined using the Planck function at the common temperature of the two materials as the weighting function.
对上述参数进行修改后,我们可以证明实际上发射率和吸收率在每个单独的频率上应该相等,而不仅仅是在平均值上。为了简化论证,我们假设e和a与方向无关。我们采用的思想实验与用于证明基尔霍夫定律的思想实验大致相同,不同的是这次我们在测试物体和黑体材料之间插入了频率选择镜,如图3.13所示。反射镜允许测试对象仅在指定频率v附近的窄带内与黑体交换辐射能。测试对象的能量预算现在为2e(v)B(v, T1)Av = 2a(v)B(v, to)Av。设T1 = To,使等温态为平衡态,我们得到e(v) = a(v)。
前面的论证是以基尔霍夫最初给出的形式提出的,是基尔霍夫定律通常给出的理由。它最终是不令人满意的,因为它将平衡热力学推理应用于一个辐射场明显脱离物质平衡的系统;在频率依赖的形式中,它调用具有假设材料属性的镜像的存在;更糟糕的是,它以辐射换热与其他换热一样来平衡温度为出发点,而我们实际上应该能够从辐射与分子相互作用的基本原理来证明这种性质。伟大的数学家大卫·希尔伯特(David Hilbert)是许多认识到这些困难的人之一;1912年
测试结束,4 |
oTo4 |
|
黑体 |
T 1 o |
|
图3.12:在所有波数的平均值上演示基尔霍夫定律的思想实验示意图。在草图上的注释中,a = a(To)和e = e(Ti)。
-
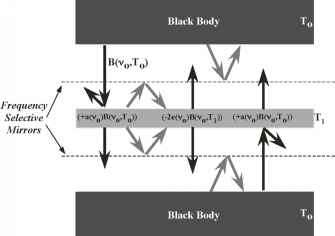
- 图3.13:用于演示频率vQ附近窄带辐射的基尔霍夫定律的思想实验示意图。细虚线代表理想的频率选择镜,它通过接近vQ的频率,但反射所有其他的而不损失。
他提出了一个正式的理由,排除了假设的理想选择镜像的影响。希尔伯特证明的物理内容是,一个人不需要一个理想的镜子,如果一个人需要足够多的材料,具有不同的吸收和发射性质,都将进入一个等温状态的平衡。尽管如此,希尔伯特的推导还是基于这样一个假设,即辐射会与每一个单独波长的物质达到平衡。当基尔霍夫用镜子做到了这一点时,希尔伯特本质上却用公理做到了这一点,让基尔霍夫定律的微观证明同样模糊不清。事实上,要对一种材料在何种情况下符合基尔霍夫定律提供精确而简洁的说明是相当困难的。这种情况在自然界和工程材料中都很常见,因为一种材料很可能储存吸收的电磁能量,然后再以完全不同的频率发射出去。我想到的一些例子是磷光材料(“在黑暗中发光”)、荧光材料(例如,当暴露在紫外线或“黑光”下时会发光的涂料)、倍频材料(用于制造绿色激光笔)以及激光本身。在自然界中,这样的现象只涉及微不足道的能量,在确定行星能量平衡方面没有已知的重要性。在这里,我们将满足于这样的陈述:所有已知的液态和固态行星物质,以及构成大气的气体,都很好地符合基尔霍夫定律,也许除了最稀薄的大气外层,那里的气体本身并不处于热力学平衡状态。
在平均应用基尔霍夫定律时,必须仔细注意用于定义平均吸收率的加权函数。例如,基于事件太阳光谱在美国,地球的平均反照率约为0.3,因此平均吸收率为0.7。这是否意味着地球的平均辐射率也必须是0.7 ?事实上,不能得出这样的结论,因为基尔霍夫定律只要求在相同频率上平均时,平均发射率和平均吸收率相同加权函数.地球的大部分热辐射都是红外线,而不是可见光。基尔霍夫定律确实要求可见光波长的发射率为0.7,但地球在这一波段的净热发射与红外相比微不足道,对地球的净发射几乎没有贡献。具体地说,普朗克函数表明,在255K时,可见光波长的发射比红外波长的发射小约10-19倍。因此,如果红外发射部分区域为100W/m2时,可见发射量仅为10 ~ 17w /m。使用AE = hv来估计可见光光子的能量,我们发现这相当于每平方米辐射表面每秒只发射50个可见光光子。可见光微弱的辐射热不应与大得多的辐射通量相混淆反射太阳辐射.
e < 1是基尔霍夫定律的一个推论。如果发射率大于单位,那么根据基尔霍夫定律,吸收率也必须大于单位。因此,物体在单位时间内吸收的能量将大于入射辐射传递给它的能量。根据能量守恒,这就意味着内能源的存在。然而,任何内能源最终都会被耗尽,违反了系统处于可以无限期保持的平衡状态的假设。
继续阅读:光学厚度和史瓦西方程
这篇文章有用吗?



