理想气体基础知识
气体是一种物质,在这种物质中,除了偶尔发生碰撞外,单个分子可以独立地自由运动。大多数时候,单个分子都在自由飞行,不受相邻分子的影响。气体与液体和固体的不同之处在于,相邻分子之间的力(在一段时间内的平均力)非常弱,因为与单个气体分子的典型分子间距离相比,分子间力的距离很短。
如图2.1所示,如果将一个假想的薄板垂直放置在气体中,就会有一个力从每一侧施加在薄板上。插入平面两侧的力相等;否则,如果相对两侧的力不平衡,板块就会经历加速度。在平板左侧的力是由分子撞击平板左面并反弹时的反射引起的。这些冲动的力量是如此频繁以致于宏观尺度力是有效稳定的。力垂直于面,无论面如何朝向,力的值都是相同的。这可以通过考虑与壁面的碰撞和没有动量平行于平面传递的趋势来看出。在平面上单位面积上的力的垂直分量称为压力。力的切向分量抵消了(当与墙壁多次碰撞时取平均值),因此当与表面多次碰撞取平均值时,力的切向分量就消失了。压强的单位是牛顿每平方米或Nm-2;1 Nm-2称为帕斯卡,缩写为Pa。大气科学家使用hPa(百帕1百帕= 100帕)或等效的mb(毫巴)。更合适的单位是kPa,但在实践中使用得并不多。1牛顿是在1kg质量上保持1m s-2加速度所必需的力。 The units of force may be decomposed to kg m s-2.
气体的状态由三个量来表征:压强p;(质量)密度,p(注意,对密度的认识等同于对密度的认识
气体中垂直板上的力
气体中垂直板上的力
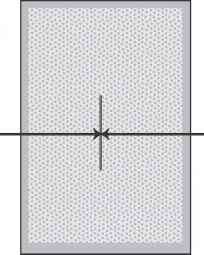
图2.1气体在垂直方向的薄板上施加的力示意图。由于板不受合力,FL = -FR。
图2.1气体在垂直方向的薄板上施加的力示意图。由于板不受合力,FL = -FR。
f f l r体积对于给定质量的单相系统,p = M/V);温度T(开尔文)一般来说,这三个变量之间有一个数学关系,或热力学坐标,称为状态方程。重要的是要记住,在热力学平衡状态下,气体的密度在整个体积内是均匀的。
数密度n0是单位体积内的分子数([no] =分子m-3)。理想气体的状态方程由p = n0kBT[理想气体定律](2.1)给出。
其中kB称为玻尔兹曼常数:
kB = 1.381 x 10-23 JK-1分子-1。(2.2)
玻尔兹曼常数是一个与分子种类无关的普遍常数。如果足够稀释,几乎所有气体都表现为理想气体。这种情况的条件是,分子之间有很大一部分时间是分开的,因此对于一个给定的分子,分子间作用力只起很小一部分作用。这将在接下来的几节中变得更加清晰,其中一些分子间的间隔和碰撞之间的距离的估计将与分子的大小进行比较。中性分子的典型分子间作用力只有在分子半径量级的距离上才明显。这与离子物种的远程电作用力(库仑定律)形成对比,其中力的范围很长,随距离的平方反比而变化。
例2.1气体在标准温度和压力下(记为STP: p = 1atm = 1013 hPa, T = 273.16 K),它的数密度是多少?答案:n0 = p/(kBT) = 2.69 x 1025分子m-3。这个值叫做洛施米特数。□
继续阅读:平均自由程
这篇文章有用吗?