E

Northei界限电流

露头

近极的副热带环流/ QYre /线

Northei界限电流

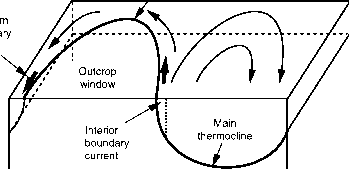
图4.18侧视图two-gyre盆地的循环,包括强大的内部边界电流和北部边界电流。

强大的埃克曼上升流亚寒带盆地驱动更加突出等密度线露头。全球解决方案的结构如图4.18所示,包括不同的结构边界电流subtropical-subpolar盆地,如孤立的北部边界电流和孤立的西部边界电流。这些边界的结构电流可以在黄和Flierl (1987)。

在早期的研究中,风力循环主要是局限于理论建模齐次海洋或低引力模型。尽管解决方案从地球引力模型可以被解释为第一斜压模式,这些模型不能提供循环的垂直结构;因此,花费了大量精力斜压环流理论的发展,但几十年来进展非常缓慢。为了真正理解新理论在1980年代开发的,我们将复习的知识海洋环流在1970年代末。通过学习历史的科学,我们希望变得更聪明下次我们面临一个新的挑战。有时看起来容易理解的理论已经被证明,但它总是更难找到并证明一个新的理论。

风力循环在分层模型

均质模型和地球引力模型

风力循环在盆地内部流可以被描述为斯维德鲁普(1947)动力学。这就是著名的斯维德鲁普关系,它是一个涡度平衡。注意,减少重力不出现在斯维德鲁普关系,所以它不会真的不管

4.1.5地下一层的谜题关于运动模型是一个齐次模型,使用的斯维德鲁普(1947),或者一个失重4.1.2节中使用的模型。在副热带环流,风应力旋度是负的,所以室内流必须向南移动行星涡度更低。

内部流程必须由某种封闭的边界层。我们有著名的西部边界理论,包括Stommel(1948)边界层和芒克(1950)边界层。

东部边界块吗地转流在地下一层吗?

东部边界的no-throughflow边界条件得到地下一层是一个强大的障碍。Rooth et al。(1978)提出了一个看似令人信服的论点基于一个潜在的涡度约束应用于地下一层。事实上,他们的论点的灵感来自于有趣的结果从以下数值模拟基于三层模型的Suginohara (1973)。

数值模型可以解释的本质而言,2 2层模型,对基本方程:

-fh1V1 = - g 'hi胡(Y + h2x) + tx (4.132)

(h1u1) x + y = 0(高压)(4.133)

嗨和h2层厚度,g = g (p3 - p2) / p是减少重力,Y = (p3 - p1) / (p2 - p1)。稍后解释说,这个系统的第一积分,即。正压解决方案,h1U1 + h2U2,可以找到从涡度平衡。然而,我们需要一个解决方案的约束来确定斜压结构。

Suginohara试图解决这个问题数值减少一组两个常微分方程,使用x作为独立的变量。b Cross-differentiating动量方程(4.132,4.132)和(4.134,4.134 b),我们获得涡度方程,进一步操纵会导致两个常微分方程g’(Y h1 + f-h2 ^ j h1x + g (h1 - fh1y) h2x = rx - f Tyx (4.136)

g ^ h2 - f-h2 j h1x + g ^ ^ h2 + f h1y) h2x = 0 (4.137)

假设边界条件指定的东部边界——比如说h1和h2常数沿东部边界——这两个方程可以改写有限差分形式。通过从东部边界向西行进,可能会找到解决底层的运动,至于对上表面。通过这种方式,可以在地下一层运动,所建议的一些数值试验。

一个模型与地下海洋层运动是一个非常有趣的结果,这促使Rooth和他的同事进一步探索的问题是否可以设置地下一层在一个无粘性流体模型的运动。Rooth et al。(1978)开始从理论论证基于潜在的涡度方程。容易证明,这些潜在的涡度方程两层是

因此,潜在的涡度的上层沿着流线变化由于埃克曼的直接力泵;然而,第二层是规避Ekman抽的直接力的影响。因此,第二层中潜在的涡度守恒地转流线,即。,流线必须遵循地转的轮廓。

然而,东部边界的存在块所有地转地下一层的轮廓。从所有可能的流动在第二层必须遵循潜在的涡量等值线,地转由东部边界轮廓的堵塞意味着所有可能的在地下流动层阻止了。

上面讨论的两种方法是完全相反的,关于的问题是否有运动在地下一层。现在我们可以看到第一种方法中的一些缺陷。附近的东部边界,第二层是停滞不前。如果第二层是在运动的地方远离东部边界,然后会有一个边界分离这两个地区。因此,简单的向西行进可能违反物理定律的穿越边界分离地转来自东部边界的轮廓和那些来自其他地方。在数学术语,问题是双曲型,所以最好是用有限差分特征坐标;否则,数值方案可能产生错误的解决方案,因为该计划违反了双曲方程信号规律。

地转的东部边界封锁轮廓似乎是一个简单的和非常吸引人的论点。从这样一个有力的论据,可以跳的结论是,在第二层就没有运动,因为所有这些地转轮廓被东部边界,所以就没有运动在所有这些地下层。

惯性失控齐次海洋模型的解决方案

另一个疑问是齐次海洋相关模型。在过去的几十年里,人们已经研究了齐次海洋数值解模型,并发现当解决方案进入高度非线性机制,解决方案看起来很不现实的。例如,Ierley和原版雕像(1995)研究了下列情形。的正压

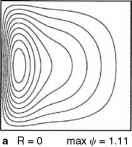
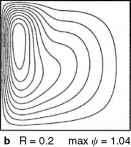
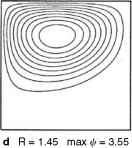
图4.19 streamfunction说明单调过渡的一个序列线性蒙克的解决方案(R = 0)高度非线性环流的解决方案(R =)固定粘度,Sm = 0.06,增加雷诺数R (Ierley和原版雕像,1995)。

涡度方程为齐次海洋模型

VA2ft + Si2J (f, V2f) + fx = SM V4f +旋度T (4.140)

J (f、Z) = fxZy - Zx财政年度,Z = Vff, u =财政年度,v =外汇,如果= ^ fUJp / L是一个参数基于惯性边界层的宽度,和SM =(:铝/ j3) L / 3 / L参数基于粘性边界层的宽度。雷诺数定义为R = S | / SM。

随着R的增加,从解决方案解决方案经过逐步转变,看起来就像发生在真正的海洋(R = 0到1)解决方案,不像我们观察海洋(R = 3.55)的情况下(图4.19)。这就是所谓的均匀的失控问题海洋模型。它表明,模型公式并不代表真正的海洋;但该模型有什么问题吗?

向上的线性quasi-geostrophic模型海洋风力循环的向上分层海洋盆地与罗斯贝波传播密切相关。这个问题首先quasi-geostrophic框架的角度讨论了安德森和吉尔(1975)。使用相同的配方,年轻(1981)讨论了一个看似疯狂的难题与持续的向上分层海洋没有西方的边界。quasi-geostrophic理论,内环流涉及相关问题解决线性向上的问题:

V f + Py + (f fz) z] t +可以= 0 (4.141)

与边界条件f | t = o = 0;f \ x = = 0;w | z = o =我们(y) B (t);w \ z = n = 0

F = F (z)是无量纲的分层,w = - F fzt / f0,我们(y)埃克曼泵对模型的上表面的海洋,0 (t) = 0 t < 0, 0 (t) = 1 t > 0是一个阶跃函数。这个问题可以通过扩张特征函数定义为解决

(FCz) z = 2 c, Cz = 0, z = 0, - h (4.142)

有无限的特征值和特征函数(kn > 0, Cn (z), n = 0, 1, 2,……)。因此,streamfunction可以正式扩展f =

Y, $ n (x, Y, t) Cn (z)和金方法可以解决问题。模态

继续阅读:E 20 E 30 E 40 50 E E 60 E

这篇文章有用吗?

0 0