2胡
潜在的涡度平衡一个封闭流线(或整个盆地)之间的摩擦力矩(主要是生成在盆地的边缘摩擦是不小),风压力扭矩施加在盆地。因此,无论多么小的摩擦力,至关重要的是维持防御的风应力涡度平衡输入和输出摩擦。此外,一个纯粹的惯性模型是物理上不可能的,因为从风应力涡度输入不平衡的摩擦。
4.1.2节,内部解决方案是通过集成从东部边界开始,但是为什么不从西部边界?很快将显示,没有当前东部边界,所以内部解决方案是有效的一直到东墙;因此,内部的解决方案可以通过集成从东部边界开始。另一方面,有一个西方的边界层,所以我们将无法获得西方边界内部的集成解决方案。
让我们专注于亚热带盆地。水不断上涨负涡度的上界。海洋内部的循环是非常缓慢的,和相对涡度可以忽略不计;因此,水包裹向南移动的地方行星涡度更小。关闭循环,水包裹与低涡度沿东部/西部边界向北移动并最终加入内部包裹应该高涡量流的水。也就是说,水包裹必须放弃他们的负涡度地方为了保持一个稳定的循环。
在西部边界政权控制卷两个区域之间的部分通过西部边界,一个在南,一个在北方。在南部的一部分控制体积,有大量的低电位涡度的来流从海洋内部;在控制体积的北部,是高潜力的流出涡度去看海洋内部。为了平衡潜在的涡度,水必须获得积极的涡度通过横向边界或边界。因此,不管我们使用什么类型的模型,应该总是有一个地方积极vortic-ity生成通过界面或横向摩擦抗衡涡度输入从室内的风应力旋度。
涡度平衡Stommel边界层
所需的摩擦转矩平衡负面风应力扭矩对盆地内部沿西部边界生成电流是最强的,不久就会显示。强烈的边界附近的电流产生最强烈的摩擦
涡度的动态边界层
涡度平衡在一个封闭的盆地西部边界当前东部边界电流西部边界电流b东部边界电流y
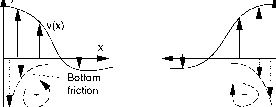
我积极
负涡度通量
图4.13涡度通量子午边界产生的电流与界面摩擦;与当前西部边界模型;b模型的东部边界电流。
我积极
负涡度通量
图4.13涡度通量子午边界产生的电流与界面摩擦;与当前西部边界模型;b模型的东部边界电流。
墙,因此积极的潜在的涡度源(图4.13)。另一方面,如果有一个边界电流附近东墙,墙附近的相应的强电流将产生一个负电位涡度;因此,东部边界电流不能扮演平衡潜在的涡度在一个封闭的盆地。
在single-moving-layer模型中,平衡内部的质量向南流动向北边界电流是必需的。假设,边界内的当前,潜在的涡度风应力和摩擦的贡献可以忽略不计,是潜在的涡度必须沿着流线是守恒的,也就是说。,(f + vx) / h = G (f)。Sincef增加向北,边界层内的潜在的涡度平衡需要一个越来越大的负相对涡度。这可以通过水平收敛边界南部政权。
类似于摩擦边界电流的情况下,只有一个惯性西部边界电流可以产生必要的负相对涡度。在这里,涡度平衡排除关闭风力的可能性环流循环有一个惯性东部边界电流。
北部的西部边界,边界流必须分开,因为它是不同的。因此,相对涡度下降沿流线;因此,一个纯粹的惯性边界电流在这个盆地的一部分,无法弥补的进一步增加行星涡度f。因此,纯惯性的西部边界电流不为西部边界北部的工作。其他一些机制必须添加到模型,如时间条件。事实上,在这个政权中尺度漩涡,被排除在我们的简单的模型上面所讨论的,是极其重要的。西方边界层的结构示意图见图4.14。
惯性西方边界层的部分关闭
与底部地形和崩溃
镜头横移装置
与底部地形和崩溃
镜头横移装置
rn向西传播。
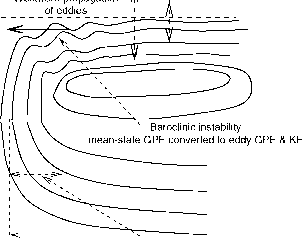
很薄的边界层摩擦^惯性西方边界层
图4.14不同动力区域在西部边界内的政权。
rn向西传播。
很薄的边界层摩擦^惯性西方边界层
图4.14不同动力区域在西部边界内的政权。
此外,基于纯惯性边界层模型不能平衡潜在的涡度在整个盆地。这是因为纯粹的惯性框架内边界电流之间没有沟通的涡度当前和固体边界,底部和侧墙等,因此该模型不能摆脱负涡度施加在盆地内部。因此,必须有其他机制的地方出口负涡度的存在,可以在整个盆地建立涡度平衡。
一个简单的低引力模型的自由表面高程Z是与层厚度h: Z = hAp / p(图4.15)。因此,重心是在一个深度(h / 2 - Sh), Sh = Z / 2 = hAp / 2 p。GPE的价值取决于参考水平的选择。目前情况下,我们选择z = - h / 2为参考电平,和GPE上面的温水温跃层是在我们使用ph = (p - Ap)的关系(h + Z),这是一个零压力梯度温跃层以下声明。相比之下,如果密度等于p均匀无处不在,相应的自由表面高程是零和GPE是零。
能量的风力循环低引力模型中重力势能
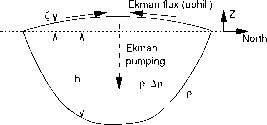
。埃克曼ySverdrup
Geostrophi ^ E S ^ ^人drnp,
。埃克曼ySverdrup
Geostrophi ^ E S ^ ^人drnp, r地转
图4.15素描的速度场和水包裹在副热带环流的运动内部的低引力模型,包括(顶部面板)的经向视图副热带环流和(下图)水平的速度矢量。请注意,地转流应该遵循h-contours。
因此,在地球引力模型中,h的增加表明自由液面高度的增加Z,这意味着增加GPE。正如3.6节中所讨论的,大量的机械能受到表层地转流的风应力等于所需的能量推动埃克曼通量艰苦的(图4.15)。这艰苦的体积通量的南部和北部边界的风力旋转推水向环流中心更高的自由表面高程;这个体积通量的收敛中间的环流将温水下行池的温暖的亚热带温跃层水盆地。Z和h的增加导致的增加GPE存储在温水泳池。
平衡风力GPE的环流
基于Stommel模型上面所讨论的,机械能的平衡方程,Eqn。(4.16),降低
U•Vh (g是什么)= u-T / p - R (u2 + v2) (4.89)
内部解决方案
在盆地内部,风应力的工作地转速度U•t > 0;因此,U•Vhh > 0, h和GPE增加下游,后反气旋的方向。换句话说,风应力输入能量和把水向高GPE的政权,箭头所描绘的顶部表面如图4.15所示。
这图也可以帮助我们理解为什么一个气旋环流在亚热带盆地是不可能的。这个盆地规模风应力与中纬度西风带和模式东风在低纬度地区,风应力工作室内的气旋环流是负的;因此,风应力不能开车气旋环流。
注意这些小差异的方向流动的南半部副热带环流如图4.15所示。图4.4所示的流线是斯维德鲁普streamfunction,所以他们包括埃克曼和通量地转流以下埃克曼层。虽然这两个组件有类似的流向北部的亚热带环流,朝赤道方向的方向是相反的副热带环流的一半。表示在图4.15的下部,埃克曼通量流向北极和地下地转当前移动向赤道。表面速度的矢量和这两个组件,从风应力和接收能量。能量输入到埃克曼层存储在亚热带盆地通过Ekman抽运光和温暖的水被推到的弓形主要温跃层,向下的箭头,如图4.15所示。
在西部边界风应力的工作项可以忽略不计,所以行星之间的平衡是涡度平流和摩擦的术语,它是负的。因此,在向北运动,水包裹必须失去GPE,即。,走向一个政权的下表面高度和浅温跃层深度,如沉重的虚线所示如图4.4所示。
分区的能量与风力环流有关
风力在上层海洋环流是最充满活力的全球海洋环流的组件。尽管这些环流的盆地规模结构可以很好的描述使用上面讨论的理论,由于涡流的贡献是排除在我们的讨论。为了理解漩涡在整个动力框架的重要性,我们需要至少粗略估计所有相关的分区形式的能源,其中包括平均流量的势能和动能和中尺度漩涡。比例分析可以为我们提供以下粗略的估计(看到吉尔等人,1974)。
首先,总动能的密度平均流量是e *,意味着ph值= 2 (u2 + v2) = 2 pg的2 h (h2 + h2) / f2«2 pg 2 hh2 / Lf2 (4.90)
overbar表示的水平平均在整个环流,h的厚度扰动,Ly ~ 1000公里是南北风动环流的长度尺度。在这个估计的贡献由于东西方梯度很小,所以它被忽略,即。,动能的子午速度是省略了估计。
可用的重力势能的密度平均流量被定义为ep,意味着= 1 pg (h2 - h”)«1 pgh2 (4.91)
因此,这两种能量的比值
意味着_ ep,意味着= ZL ^ 1000 (92)
艾克,意味着Ek,意味着^ 2
在k = ^ Jgh / f ^ 30公里半径的变形。因此,平均流量的动能在风动环流与大量的可用势能。
另一方面,中尺度涡流的势能和动能可以估计如下。如果所有的可用势能转换成的能量漩涡,中尺度能量的总能量应该一样可用势能,也就是,
Eeddy - Ep,意思是(4.93)
认为典型的中尺度涡流的规模是k - 1。一般来说,艾迪规模大于变形比k - 1 > k和涡流能量主要以势能的形式。同样的估计平均流量的动能,艾迪动能密度可以作为埃克估计,艾迪«1 pg的2 hh / 2 k-2 / f 2 (4.94)
因此,艾迪艾迪势能动能的比值
Ep,艾迪= Ep,艾迪= k_2 10 ^ (95)
艾克,艾迪艾迪Ek, k
和艾迪动能的比值平均流的动能
艾克,艾迪/ Ek,意味着(kk)«100 (4.96)
因此,艾迪动能是平均流量动能的100倍。
尽管Stommel界面摩擦模型的物理解释有时被称为模型与“底摩擦,”在现实中使用的摩擦低引力模型实际上是一种界面摩擦。这个界面摩擦被假定为线性与上层的速度成正比。因为较低的层在低引力模型被认为是停滞不前,这实际上是一个粗糙的参数化界面摩擦界面剪切速度成正比。因此这样一个Stommel模型中的参数化是一种粗糙的斜压不稳定的参数化。
因此,GPE的所谓的界面摩擦损失Stommel模型可以解释为输给西部边界内的斜压不稳定。最重要的是,通过所谓的界面摩擦机械能量损失不是转换为内部能量;相反,这种能量转化为GPE和动能维持细观漩涡。然而,斜压不稳定在海洋中似乎没有发挥至关重要的作用在盆地的西部边界。事实上,它主要发生在流出政权,如墨西哥湾流扩展或再循环;因此,物理意义的参数化仍然是争论的主题。
4.1.4帕森斯模型
介绍
在大多数风力循环模型,分层沿着指定的东部边界是先天的,和海洋内部的解决方案是在这样的一个假设。还有另一种方式看待同样的问题——而不是指定层厚度沿东部边界,可以指定一个海洋中温水的总量,并找出温跃层受到斯维德鲁普的结构关系。事实上,这是完全相同的方法在大多数数值模型用于风力循环——我们指定的水量在每个密度类别和“自旋”模型来找到解决方案符合其他动态约束。
帕森斯模型
帕森斯(1969)制定一个非常优雅的模型,试图解释墨西哥湾流分离。通过摩擦和ageostrophic而言,他的模型预测非常明确的循环在亚热带盆地。因此,像Stommel和芒克模型,这是一个分析模型,在一个封闭的盆地。
尽管帕森斯模型扩展在很多研究中,应用相同的基本假设:
•稳定循环
•两个非混相层,固定在上层的水
•降低层是无限深,一动不动
•界面摩擦速度成正比的上层。
模型是制定j-plane,和相应的基本动力和连续性方程h (u■Vh) u +高频徐= - g 'hVh +——俄罗斯(4.97)
U = (U, v)是水平速度,是一个二维的运营商和f = fo +司法院,fo = 2«罪6 (4.99)
是科氏参数。引入无量纲变量
L p f = Ljf ' f ' = fo + y ', fo = L谭6 o - 0.5 (4.100)
L和H模型的水平和垂直尺度海洋,W是风应力的规模,是地球的半径,0 o是中央纬度模型的海洋。下降后启动,无量纲方程
R0h (u■Vh) u +颗x胡= -HVhh +——欧盟(4.101)
g是什么R LW哪里
Ro = h *«1,«=》«1 * 4 = TPH energy (103)
的无量纲参数模型。在这个模型中¡x是一个关键的无量纲参数。因为没有源或沉没,streamfunction可以介绍,胡= -财政年度,高压=外汇(4.104)
边界条件是f = 0,在刚性边界(4.105)
f = 0,在h (x, y) = 0(露头线)(4.105 b)
该模型的特点是存在一个露头线简化和zero-depth线。小心处理这些边界条件在露头线是至关重要的准确描述出露地表的现象。
连续性方程可以被解释为一个积分约束d ff hdxdy = 0,即。在上层,水的总量是固定的。在无量纲形式,这种约束
为简单起见,我们使用以下额外的假设:
•风应力只有纬向分量r = (tx (y), 0)。
•室内流动惯性项可以忽略不计,即。,Ro ^ 0。
然而,我们必须保持e项,因为不能封闭循环在盆地没有摩擦。
解决方案没有露出
在这些假设下,横向动量方程
- f fx = -hhx + - + i ^ tx财政年度(4.107)
内部解决方案
忽略摩擦条件,动量方程简化为
(4.109)- f fx = -hhx +插件可以
Cross-differentiating减去这两个方程和涡度方程
利用涡度方程和积分从东部边界导致内部解决方案fi = p (1 - x)的处方(4.112)
高频= h2 + 2 k (1 - x) f2 (tx / f) y (4.113)
在那里他= const是无量纲层深度在东部边界。
西方边界层,我们引入一个拉伸边界层协调n = x / e。动量方程成为e2 x
- f fn = -hhn + - + eprx财政年度(4.114)
继续阅读:E
这篇文章有用吗?