散射的各向同性均匀球体
一个各向同性,均匀球体是最简单的有限的散射体,连着的散射理论古斯塔夫米氏的名字。这是公司附件,无视逻辑和历史每个粒子在阳光下被称为一个“米氏散射体”,从一个特定的理论和米氏散射提升有限的适用性的不劳而获的排名一般散射过程。
米氏散射并不是第一个来解决这个问题的一个任意的球体。更正确的说,他是最后一个。他给他的解决方案在现代符号和画风还解决了一个实际问题:胶体金的颜色。由于这些原因他的名字是附加到球体散射问题,尽管他的前任,尤其是洛伦茨(不与洛伦兹混淆)。这是一个例子的同名认可了最后发现者而不是第一个。
米氏散射是不是一个物理过程;米氏理论是一个在许多。严格地说,它甚至不是准确的,因为它是基于连续介质的电磁理论,本身近似,在照明的平面波无限横向程度。
由一个球体散射可以使用各种近似方法确定轴承和米氏理论:弗劳恩霍夫理论、几何光学、反常衍射理论,coupled-dipole, t矩阵方法,等等。因此是一个球体米氏散射体或反常衍射散射体或coupled-dipole散射体?可能性是无限的。
当一个物理过程可以被描述为不同的理论,这是不明智的把其中一个的名字。
有所谓的米氏和瑞利散射之间没有明显的边界。米氏理论包括瑞利(球体),这是一个限制理论严格适用只有粒子的大小缩小为零。即使对球体不加鉴别地贴上“瑞利球”,总有瑞利和米氏理论之间的偏差。阻碍一个人的思维,据说锋利的瑞利和米氏散射之间的界限,一个风险扔一些有趣的物理窗外。粒子是否米氏或瑞利散射体并不是绝对的。粒子可能是毕业于瑞利米氏状态仅仅通过改变波长照明。人们经常遇到陈述由气缸米氏散射,球状体,覆盖领域和其他nonspherical或不均匀的粒子。判断历史上,这些语句都是胡扯。米氏从未考虑过以外的任何粒子均匀球体。
逻辑似乎要求如果一个粒子是米氏散射体,然后米氏理论可以应用于散射。这个谬误的概念已经引起了并将继续造成伤害,可能是最好的原因停止指“米氏粒子”或“米氏散射”。利用米氏理论的散射粒子以外的领域,特别是在落后的方向,附近是有风险的。
通常情况下,一个更好的词比米氏或瑞利散射是可用的。如果散射分子,分子散射比瑞利散射(它本身是一个不精确的术语):前者指的是一个代理,后者理论。米氏散射体是一个不必要的贵族的名字卑微的球体。每当米氏散射体被替换为球体,结果是清晰的。如果需要限定符,一个可以添加与波长相比小或大或与波长可比。
短暂,散射的解决问题的办法任意平面均匀球体被波可以通过扩大事件,分散和内部电场和磁场在一系列的矢量球函数(一般方程的解决方案电磁场在球坐标)。这些扩展函数的系数选择的切向分量的字段是连续球面。因此这散射问题是正式相同的反射和折射,因为接口,虽然球问题更加复杂,因为分散和内部字段不是平面。
可观测量表达的复杂散射系数一个和bn的扩张分散电场和磁场。例如,横截面是无穷级数:
= E (2 n + ^ l”™!2 + 16种»| 2}- (3.133)
散射系数可以写
_ (Dn (mx) / m + n / x]“tpn (x) - tpn -
[Dn (mx) / m + n / x \ ^ n (x) -£„_i (x)”
b _ [mDn (mx) + n / x] tpn (x) - v > n_i (x) ^
^ n和在哪里Riccati-Bessel函数和对数导数是什么
尺寸参数x是ka,球的半径和k的波数入射辐射在周围介质(假定nonabsorbing);m是复杂的折射率(在前面的小节讨论)的球相对于周围介质的折射率(真正的)。方程(3.134)-(3.136)是一个在许多方面写的散射系数,其中一些比另一些更适合计算。在任何方向散射入射光的偏振状态也由散射系数。
一个好的经验法则是,数量所需的条件收敛级数的方程式。(3.132)和(3.133)是大约尺寸参数(2 na / X)。雨滴的订单1毫米,因此它们的大小参数在可见光波段10000订单。彩虹摆脱米氏理论的细节但在加法10000条款的成本,这就是为什么我们经常诉诸近似如几何光学,它揭示了一些但不是全部功能的彩虹(见秒。8.4.2)。描述所有的特性我们不得不诉诸米氏理论,甚至它不够好,因为雨滴不是球体(云滴),及其偏离球形可观察到的后果。,这使我们的“等效球面”的概念,竞争对手的搜索食谱的炼金术士的追求把贱金属变成黄金。唉,就像没有这样的配方,没有所谓的一个等价的球体,有同样的散射和吸收特性对于粒子。首先,这种粒子是由它不是什么,唯一的特征由所有对于粒子共享。猫是任何动物,它不是一只猫,它带给了我们一个动物园住房从大象和长颈鹿豪猪和鼩。因为一组随机取向对于粒子具有相同的对称性作为一个球体,它有时被认为(系综平均)收集的散射特性相同的适当选择“等效球”。 Not true. The error here resides in confusing the symmetry of an ensemble of particles with that of a single particle. No matter what incantation is used for conjuring the properties of an equivalent sphere, differences between scattering and absorption by it and by a non-spherical particle always exist. Sometimes these differences are huge, sometimes not. Beware of equivalent spheres.
在大萧条数学家是三角函数和其他函数计算工作表。他们的劳动的结果现在在图书馆收集灰尘。今天,这些表可以生成更准确地在几分钟内袖珍计算器。类似的命运降落在米氏计算。之前快电脑是便宜的,表散射函数的有限范围的尺寸参数和折射率发表。今天,这些表在个人电脑可以在几分钟内生成。算法更有价值和持久的比表计算,这是最无用的除了检查有人开发和测试算法。米氏计算的主要任务是计算方程式中的函数。(3.134)和(3.135)和加法系列等
方程式。(3.132)和(3.133)。如今米氏代码比比皆是。你可以找到他们在书中,在互联网上,可能在高档超市结帐。
横截面与半径或波长传达物理信息;效率和尺寸参数传递的数学信息。尺寸参数与物理内容小于它的组件是一个变量,整个被比它各部分的总和。此外,横截面与尺寸参数(或它的逆)并不等同于横截面和波长。除了梦境,折射率随波长和米氏系数取决于x和m,波长被明确的在第一,隐含在第二。
粒子比波长小得多
足够小x和m \ \ x,球体的体积灭绝和散射横截面近似
Csca / v
2 aiy3v
v是波长的粒子体积和周围的(可以忽略吸收)材料领域。类似的方程,特别是体积依赖,为小,均匀粒子的形状。注意情商的相似性。(3.138),(3.114)式。由薄板进行反思。这些方程的来源是无名的悖论,不时地挖出,一具尸体永远安息。如果球体nonab-sorbing真正(m), Eq。(3.137)收益率消失灭绝截面而Eq。(3.138)收益率non-vanishing散射截面,然而灭绝不能小于散射。两个方程得到幂级数的大小参数x,方程(3.137)中第一项系列。是一致的,横截面必须扩展到相同的顺序在x。在这样做时,矛盾就消失了。事实上,它根本就不存在。
另一个毫无意义的悖论源自的好奇定义雷达backscatter-ing截面4 n次微分散射截面向后的方向。小球体这导致反向散射截面50%大于总散射截面,乍一看确实是抓头的原因。雷达反射率的总和是雷达后向散射截面的散射单元体积。
图3.9显示了散射和吸收横截面水滴的直径20点在六波长几十年。波长大于直径,散射是一个线性函数(logarimthic情节)的波长与斜率大约4,依照Eq (3.138)。在这些波长,灭绝是由吸收,所以根据情商。(3.137),吸收应该减少(再一次,在对数图)线性斜率为1。这是不发生(见图3.9),因为复杂的折射率也随波长(图3.8)。
尽管情商。(3.138)是一个小粒子的散射截面,它仍然必须包含足够的分子可以被指定一个折射率(分子不能)。尽管如此,
让我们抛下谨慎和分子大小推断这个方程。如果我们使用水的折射率和颗粒直径0.3海里,我们获得一个散射截面中间的可见光谱的0.7 x 10 - 19 pm2。空气(平均超过所有分子但主要氮)约为4.6 x 10 - 19 pm2。这不是糟糕的协议考虑到散射截面的水蒸气小于空气(氮气和氧气),分子直径显示不是很好,散射截面取决于直径的6次方。
粒子比波长大得多
另一个矛盾有一个名字:灭绝悖论。紧凑的粒子,如一个球体,灭绝截面有极限值lim CWt = 2 g, (3.139)
那里是一个线性尺寸的粒子(一个球体的半径)和G投影几何横截面积。情商因素2。(3.139)引起了人们汗:根据几何光学应该是1。方程(3.139)似乎暗示一个大(与波长相比)粒子的裤子太大了两倍。几何光学,根据这一束光想象是一束光,被认为是一个很好的近似的对象比波长大得多。因此每一个射线相交一个粒子几何区域G应该吸收或倾斜,而光线之外这个阴影区应该通过毫发无损。问题是,光线不存在不管有限粒子有多大,它总是展览一些离职,可能小,从几何光学,在这种情况下非常接近前进的方向。
之前我们提到(并显示在图3.13)散射更向前方向的峰值更大的粒子。理论计算散射光从一束(monodirec-tional)无论多小散射角。测量的全部灭绝截面无限期大粒子需要微乎其微接收角的探测器。但任何真正的探测器一定near-forward散射光的收集一些,这样可以减少灭绝截面的理论最大值。当near-forward散射光中包含测量、限制灭绝截面(Eq。(3.139)]下降到G,如预期的基础上,通过几何光学直觉型。之间的区别是真正的和理想的。一个真正的灭绝截面探测器措施
农协。cc, Cext是理想的(理论)灭绝截面和集成验收立体角的探测器。
在图3.9中两个渐近线,G和2 G,由虚线所示。在充分短的波长,灭绝是由散射,散射截面确实接近渐近线2 g。但也要注意在一系列中间波长散射和吸收横截面都约等于G。
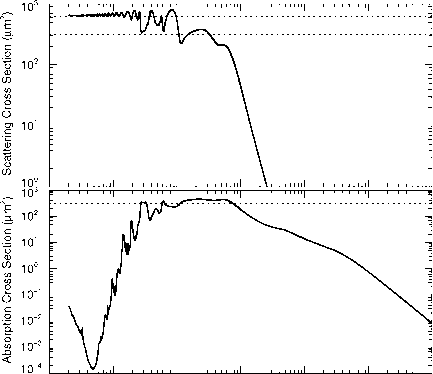
图3.9:散射(顶面板)和吸收(底板)横截面的水滴直径20 | m。两个水平虚线在前面板显示几何横截面积和两次这个区域;在底部面板水平虚线表示几何横截面积。
波长
图3.9:散射(顶面板)和吸收(底板)横截面的水滴直径20 | m。两个水平虚线在前面板显示几何横截面积和两次这个区域;在底部面板水平虚线表示几何横截面积。
这些难以捉摸的小水滴
我们国家1.4.2节,关于什么是云滴的平均规模应该对纵声大笑,但只是勾勒出的原因。现在我们可以进一步扩大在这个带着这部分的结果。
云滴与可见辐射的波长相比很大但是与微波和雷达相比较小。可见波长的水滴散射截面与液滴直径的平方。灭绝是由散射(图3.9)和灭绝几乎是渐近值(Eq。(3.139)]。然而,微波波长的灭绝主要是吸收,因此从情商。(3.137),吸收截面与液滴直径成正比的立方。但在这些波长的散射截面,因此也雷达后向散射截面,是propor -

0 20 40 60 80 100 120 140 160 180 200
直径(pm)
图3.10:前面板显示的原位测量液滴大小分布数量层云。从这对横截面面积分布的分布函数,体积,和体积的平方。
0 20 40 60 80 100 120 140 160 180 200
直径(pm)
图3.10:前面板显示了原位测量液滴大小分布数量的层云。从这对横截面面积分布的分布函数,体积,和体积的平方。
一对液滴直径的6次方。这些不同的依赖性在大小推断产生深远的影响远程辐射测量液滴属性。
直接测量用一架飞机飞过(水)层云宾夕法尼亚州立大学附近,显示在图3.10中,它显示了水滴的数量分布,从区域(直径的平方),体积(立方直径),和体积的平方(直径的6次方)分布计算。每单位体积数密度分布(水滴)高峰在6点左右。直径大于约40点,数密度大约是六十年小于峰值。可见辐射的散射峰下午16点,在直径数密度大于两倍不到它的峰值。体积分布的峰值是进一步转变,大约20点。虽然方量分布的峰值是转移到只有22点,液滴比约40点雷达后向散射信号做出更多贡献,比小水滴即使它们丰富一百万倍。
图3.10考虑如何令人沮丧的消息传达给任何人希望的推断远程辐射测量液滴大小分布。分布是最大的数量较小的尺寸,而属性的任何方案基于远程推断大小可能分布完全不同。例如,如果最小的水滴(< 6点)要删除完全从云端,体积,和更多的v平方分布不会想念他们。需要为了检测(远程)的小水滴是一些电磁属性只取决于数密度,或者在最坏的情况下,在直径。但这样的属性似乎并不存在。
继续阅读:为进一步阅读Tzr参考和建议
这篇文章有用吗?