Xa Xb aXX Vyy Xb136
这个估计的方差
°= (a + a; 2) 1。(13.7)
尽管它很简单,这个例子展示了一些先进的线性数据同化方法的关键特性。首先,注意最优估计在情商。(13.6)
是一个线性组合的背景xb和剩余y—xb。这个词
Sxa = a2x (a2x + o2y) - \ y - xb) (13.8)
被称为分析增量。注意限制牛0(完美的背景)和y ^ 0°(完美的数据),而收益率xa = xb和xa = y,分别。此外,估计的方差最优(13.7)小于背景或数据的方差分别;结合信息从背景和观测结果减少了不确定性。
13.3.2.1示例2:一个向量的估计(最优插值)
按照惯例,概括矢量的估计上面的例子中,假设所有错误高斯。这是在高斯平滑,形成了许多估计算法的基础。当未知向量代表值在一个常规的空间网格,这个过程被称为最优插值(布雷瑟et al . 1976年)。这里使用的符号是Ide et al。(1997)。
假定一个愿望来估计一个向量x e RN,给定一个背景xb,和一个向量的观察y e RM。最优插值(也称为客观分析)通常是为了顺利执行插入稀疏观测到均匀间隔的空间网格,在这种情况下,x可能代表说,海面高度网格点的值。假设观测向量的每个元素y ={一}f = x可以表示为一个线性算子的作用在x (ti),
h;e RlxN。例如,h .可能提取x的值在空间坐标($ p (x)地理经度坐标。接下来,定义矩阵h e RM xN通过收集测量,y = Hx运营商在一起。更普遍的是,观测算子H地图模型变量x的一个等价观测向量,的位置和特征(如单位)测量。
应用贝叶斯定理,它是必要的状态的概率密度x - xb和测量误差年代= y - h)。这些都应认为是多元高斯0表示;B e RNxN的协方差,即
< (x - xb) (x - xb) T B) = (13.10)
和e r e rmxM来标示的协方差。应用情商。(13.2),发现x y的条件是成正比的pdf exp (- 1 j (x))
J (x) = (x - xb) TB-1 (x - xb) + (y - Hx) TR-1 (y - Hx), (13.11)
这是目标函数,形成了所谓的变分资料同化的基础。目标函数,也称为成本函数或罚函数,将最小化对向量x。
的线性代数,一发现值x = xa最小化J是xa = xb + K (y - Hxb), (13.12)
分析的增量Sxa = K (y - Hxb)和K的吗
K = BHr (HBHr + R) 1。(13.13)
完整的分析误差的表达式,xa的误差协方差,pa e rNxN来标示
Pa = (b - 1 +人力资源R-1H) 1。(13.14)
备注:
1。方程(13.12)可以推导出最佳线性无偏估计量(蓝色),最大限度地减少预期错误(eTK (xa - x)) 2,其中ek e Rw是基向量指向方向k。同样的,估计也最小化期望均方误差Tr ((xa - x) (xa - x) T) / N。这些事实是蓝色的等价的基础,变分和卡尔曼模型dyanamics时基于过滤器的状态估计和测量运营商都是线性的。
2。当最优插值用于实践中,上述公式往往简化计算每个网格点,分析从附近的数据在一些影响半径Lorenc (1986);戴利(1991)。
3所示。J (x)上面写的也叫罚函数或成本函数。分析领域xa是它的最小值。同时,1 j是负对数似当错误是高斯函数。
4所示。因为H是线性的,J是凸和拥有一个独特的最低。H代表一个非线性算子时,可能存在多个极小值。
5。额外的限制可能被添加到目标函数,说,抑制某些动力学。这些可以大大解决方案过程复杂化,可能掩盖了R B或未能正确占的协方差结构背景和测量误差。
6。目标函数的条件数指的是比例最大的海赛矩阵的最小特征值的二阶导数的J .特征值谱黑森原则可以理解为曲率的轴iso-surfaces J。
7所示。关于高斯假设错误时是正确的,海赛矩阵H = d2 J / dx2和分析误差协方差相关Pa的H - Pa = 1。
8。上面的形式主义可以应用到连续的领域,而不是在RN向量。在这种情况下x通常是一个矢量函数然后惩罚功能和J。最低V J = 0的平稳性条件必须使用变分法导出;结果是欧拉方程。有关系密切的平滑样条函数理论,b - 1是positive-definite-symmetric微分算子(·1990)。
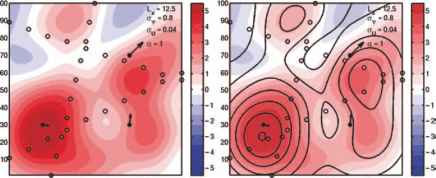
2044 60 80 100 20 40 60 80 100
图13.4例2:最优插值。左边的面板显示了海面高度^ (x, y)估计从观察n的理想化的卫星地面跟踪(打开黑色圆圈充满表示测量值),并从三个观察的表面流(黑点装满箭)。右边的面板显示了插入字段(黑色轮廓)覆盖的海面高度。参数在右上角出现在文本中定义。一个可以看到大规模的流动特性,如大anti-cyclonic艾迪,重建在插入字段
2044 60 80 100 20 40 60 80 100
图13.4例2:最优插值。左边的面板显示了海面高度^ (x, y)估计从观察n的理想化的卫星地面跟踪(打开黑色圆圈充满表示测量值),和从三个观察的表面电流(黑点装满箭)。右边的面板显示了插入字段(黑色轮廓)覆盖的海面高度。参数在右上角出现在文本中定义。一个可以看到大规模的流动特性,如大anti-cyclonic艾迪,重建在插入字段
9。连续字段的解释而言是至关重要的正确理解目标函数作为模型的调节分辨率增加连续极限(班纳特和Budgell 1987;班尼特1992年)。线性代数的语言不适合分析空间规律(可微性)分析的增量。
最优插值的一个例子是显示在图13.4。估计向量x是海面高度经常1公里网格内盒尺寸100公里100公里。表示的海面高度场^ (x, y),元素的x ^ (xj, yj)网格。在这个理想化的设置有30的观察海面高度
因为我= 1,……沿着三个卫星地面轨道,30(着色点)。假设电流地转平衡表面压力梯度,有3近地表的观测电流与箭头(黑点)。u-component给出的
继续阅读:伴随数据同化方法
这篇文章有用吗?