热力学相平衡的雪

散装平衡温度在一个纯粹的水系统

热力学三个之间的关系确定晶粒生长和水阶段变质的雪。是否存在复合水以冰的形式存在,水或水蒸气取决于其温度(T)和压力(p)、相图在图2.5所示。蒸发(A)的曲线,升华(B)和(C)融化跟踪点两大体积的水在热力学平衡相共存。在三相点所有三个阶段共存,温度是0.01°C和hPa蒸汽压为6.1112。雷竞技csgo这不是一样普通冰的熔点,发生在温度0°C和1大气压力(1013.25 hPa)。蒸汽在亚稳平衡对沿虚线的过冷水,扩展了蒸发曲线低于0.01°C。

空气充满了蒸汽平衡饱和,增加更多的蒸汽会引起冷凝。三相点以下,水的饱和蒸汽压平衡对总是超过对冰,从而支持雪晶的生长,如2.1.2节中所讨论的那样。超饱和蒸汽压力达到最大值-11.8°C(见图2.5)。过度饱和与冰的蒸汽平衡对水在0°C从0%增加到46%在-40°C。

相图中的曲线是由整合克劳修斯——克拉珀龙方程方程dp Lji

i和j是两个阶段,T是开尔文,V是体积单位质量(或互惠密度)的阶段,和L潜热。在0°C潜在的热害怕的融合(谎言),蒸发(L v),和升华(Liv),分别3.335 x 105, 2.505 x 106和2.838 x 106公斤。L适度取决于温度(见Pruppacher·凯尔特,1997年,p . 97)。对理想气体常数Lkv,方程(2.1)的集成提供了近似表达式的蒸发和升华曲线形式

T是在°C。pvsat, k是饱和蒸汽压(hPa)对冰和水,和系数a、b和c是经验适合温度范围。-40和0°C之间,巴克(1981)建议表达式

pv。分= (1.0007 + (3.46 x 10-6pa)) 6.1121 expf ^ \ (2.3)

pv,坐,我= (1.0003 + (4.18 x 10-6pa)) 6.11雷竞技csgo15 exp (——) (2.4)

含水饱和度和-50和0°C之间

冰饱和,pa是大气压力(hPa)。最初的系数在两个表达式是一个轻微的校正因子时使用气相是潮湿的空气,而不是纯水蒸汽。

曲率的影响在雪的t - p曲线相平衡克劳修斯——克拉珀龙方程乘飞机是相分离的表面。这些平衡条件改变时,表面是弯曲的,水与冰颗粒或半月板一样湿雪(见图2.4)。因为工作需要扩展界面电影,凸接口背后的阶段经验更高的能量和压力。压差(j =π- pj)在曲面是由拉普拉斯方程是pj = 1, (2.5)

其中一个j是界面表面张力和Z ij是均值曲率半径(Defay et al ., 1966年,p . 6 Dullien, 1992年,页119 - 122)。表面张力^,aiv,

表2.3比饱和压力对冰球体,在飞机表面。

表2.3比饱和压力对冰球体,在飞机表面。

rg (1 x三分	米)	10 - 6	纯	10-4	三分	10 - 2	10 - 1
pv,坐,我/ pv,坐,我	0°C	6.05	1.20	1.018	1.002	1.0002	1.000 02
-20°C		6.97	1.21	1.020	1.002	1.0002	1.000 02

和oag平均是0.028,0.104和0.076 Nm-1在0°C和随温度变化强烈(Pruppacher, 1995)。高表面张力和更严格的曲率导致更大压力差异。

对于曲面,克劳修斯——克拉珀龙方程方程推广到Gibbs-Duhem方程(Colbeck Defay et al ., 1966年,1980年)

有关阶段的压力通过拉普拉斯方程,Gibbs-Duhem方程集开尔文的平衡蒸汽压的表达式p 'vsat k /曲面

“2 okv 1

pv、坐、k _ pv,坐,k exp

这里pv坐在k平衡压力在一个平面上,pk是水的密度或冰,房车水蒸气的气体常数(J = 461.50公斤k - 1)和T开尔文。方程(2.7)预计,将在小冰粒子或更高的蒸汽压较高的精细结构曲率。表2.3显示了p !v坐在k / pv坐k冰不同半径的球体(Z¡v = rg)这样的温度在0到-20°C。

Gibbs-Duhem方程也预言了融化温度的雪。对于两相水冰系统,如被水浸透的雪或口袋内被水浸透的雪包(粮食在图2.6),水从毛细管压力计算压力,帕特= pa - pt,冰的拉普拉斯方程。2.4.2节中我们讨论毛细管压力。熔点萧条被水浸透的雪从而减少直接与毛细管压力和负与颗粒半径

273.15

2欧六世的

因此,大冰颗粒有较高的熔化温度和将增长为代价更小的颗粒。在完全饱和的积雪,空气/水界面是平的,第一项在方程(2.8)下降。

较低的含水量,液体通常配置为摆动的戒指对two-grain联系人或静脉three-grain集群,如无花果。2.6 b和c r g

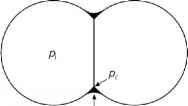
Ca«Pa

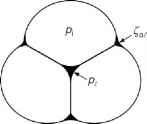
图2.6。压力的关系和形状的水湿雪夹杂物,在pk的压力和Z ai的曲率半径是空气/水界面。(a)饱和区雪高含水量(规模)。(b) Two-grain接触摆动的包含在雪低含水量(修改从Colbeck转载,1979;1979年版权许可爱思唯尔)。(c)与vein-fillet Three-grain集群包含在雪含水量较低(1979年从Colbeck转载,在b)。

(Colbeck, 1979)。与空气占据的孔隙空间,在冰压力计算拉普拉斯方程应用到冰/空气界面和熔点抑郁成为(Defay et al ., 1966;Colbeck, 1979)

273.15

2 ctw六世

因为在(2.9)第二项很小,Td主要取决于毛细管压力,增加与减少液态水。

熔化温度的预测方程(2.8)和(2.9)抑郁仅略低于0°C的大部分价值,因此,对于能量平衡计算,表面张力和曲率对温度的影响是微不足道的。然而,他们是最重要的雪变质和粘结强度。在低含水量、颗粒表面的熔化温度低于冰债券,将热量从债券,使它们生长和加强(Colbeck, 1979)。当雪颗粒完全被水包围,有一个热力学和逆转热量流动对债券,导致它们融化。饱和或泥泞的区域在雪因此无黏性和r g的力量。杂质在融水进一步打压KfM的熔化温度,在KF (K = 1.855公斤mol-1)是水的冰点测定法的常数和M的质量摩尔浓度是物种(每千克溶剂的溶质摩尔数)。

继续阅读:雪变质

这篇文章有用吗?

0 0