基本概念

最后更新于2022年12月16日星期五|表面温度

大气可以被认为是粒子的混合体，有些粒子吸收，有些粒子散射，有些粒子两者兼而有之。粒子可以是分子，也可以是凝聚态物质的宏观粒子，如云滴或尘埃粒子。人们从单个粒子的吸收和散射特性建立起整个大气的吸收和散射特性。为了与前几章的用法保持一致，我们最终将按照单位质量大气的散射特性来描述大气成分对辐射的影响，就像我们对吸收系数所做的那样。

考虑一束平行的单色(单频)光束，其通量为F / W/m2，沿特定方向行进。当光束遇到有限范围的粒子时，一定

: 跨国公司

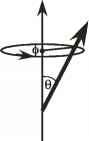
: 图5.1:传播角(左)和散射角(右)的定义

一定量的通量会被吸收，一定量的通量会散射到其他角度。能量从光束中被带走的速率吸收和散射可以用具有面积尺寸的系数来表示，这些系数被称为截面。能量吸收率为Fxabs， \abs为吸收截面，能量向其他方向散射的速率为Fxsca，其中xsca为散射截面1。散射和吸收截面可能与实际情况大不相同横截面面积物体的。截面可以被认为是横截面区域假设的等效物体，吸收或散射所有击中物体的光，同时让光束的其余部分不受干扰地通过。散射截面与散射体实际横截面面积的比值称为散射效率, Qsca。对于半径为r的球形粒子，Qsca = xsca/(nr2)。吸收效率的定义类似。对于球形粒子，截面与辐射射向粒子的角度无关。对于非球形粒子，单个粒子的横截面取决于角度，但典型的物理情况包括以随机方向呈现的粒子集合的散射。在这种情况下，我们可以平均所有方向，并表示平均散射或吸收的横截面为等效球。如果粒子不是随机定向的，这种方法就会失效，就像板状冰晶在下落时通过摩擦阻力而定向一样。粒子的单次散射反照率是入射光束通过散射损失的通量与净通量损失的比值。用符号upo表示单个粒子的单次散射反照率，我们有upo = xsca/(xsca + xabs)。稍后我们将介绍整个介质的单散射反照率。 The cross sections for particles or molecules can be measured in the laboratory, and often can be computed from basic physical principles.

由于我们要处理的辐射场一般分布在一个频率和方向范围内，而不是单色和单向的，我们将根据我在第3章和第4章中介绍的光谱辐照度来编写方程。回想一下，如果光谱辐照度在给定点为I((9,4 >)， v)，那么Idlldv是频带dv的辐射通量，其旅行方向在一个关于(9，^>)方向的立体角dl内，穿过垂直于旅行方向的平面。要将上一段的结果应用于均匀分布的辐射，只需用Idlldv代替入射通量F。

更常用的表示横截面的符号是a，但在我们的主题中，这个符号是为斯特凡-玻尔兹曼常数保留的。我们可以认为x代表xp^aa-section。

在前面的章节中，我们将做平面平行假设，并且假设I只通过压强依赖于位置。假设在某压力水平p附近，每单位大气质量有N个i型散射体，每个散射体的质量为mj。假设照射在层上的光沿垂直方向以0角传播。然后，取厚度足够小，可以忽略多次散射的层dp，入射光束由于吸收和散射到不同角度的能量损失率为dp dp 11 1

N■(Xabs,i + Xsca,i)IdQ;dv =——qi■(-Xabs,i +——Xsca,i)IdQ。dv (5.1)

t\ V/Y abs,i i /\sca,ii~---------ft n V/ \。Abs,i i g cos6g cos6mi其中qi是所讨论粒子的质量浓度。由此我们可以定义物质的吸收系数Ki = Xabs,i/mi，单位为m2/kg。这个吸收系数与我们在第四章中定义的气体吸收相同。上述方程中的附加项描述了入射光束由于散射而损失的能量。我们不会为这一项引入单独的符号，因为散射是最常见的特征是横截面本身。

如果大气中只有一种光学活性物质i，我们用方程dr * 1.1定义垂直方向上的光学深度。

Dp g mi

由于吸收和散射特性通常取决于波数，光学深度通常是波数的函数，尽管当我们希望特别注意波数相关性时，我们只会在t*后面附加波数下标。如果有很多类型的散射体和吸收体——其中可能包括单一物质但大小不同的粒子——那么我们通过对所有物种的总和来定义光学深度。即dr * 1,1

= - g(K + 2。-Xsca iqi) (5.3)

净吸收系数是多少

然后我们将介质的单散射反照率定义为

对(k,u0)构成了介质吸收和散射特性的基本描述。两者都是典型的波长和高度的函数，也可以直接是压力和温度的函数。如果介质只由单一类型的粒子组成，悬浮粒子的气体既不吸收也不散射，则uo = upo。一般来说，介质的单次散射反照率取决于吸收剂和散射剂的混合。例如，大气可能由完美散射体(upo = 1)的云粒子和强温室气体(吸收体)的混合物组成。在这种情况下，即使云粒子浓度保持不变，uo也会随着温室气体浓度的增加而下降。

利用光学深度的定义，光束能量损失率的方程5.1可以简单地重写为dl = -Idr*/ cos 6。由于通量的垂直分量是I cos 6，这个表达式可以被重铸为垂直通量损失率的表达式，即dI cos 0 = -Idr * (5.6)

散射损失的比例为，而吸收损失的比例为1 - wo。由于吸收而损失的能量的命运不同于由于散射而损失的能量的命运。前者消失在了大气的热量，而从一个光束散射而损失的能量在其他一系列方向上以通量的形式重新出现，因此我们需要分别跟踪这两种损失机制。光束在给定方向上的损失由两个源项抵消:一个来自热发射，另一个来自其他方向的散射。热发射项与普朗克函数成比例，可以用类似于推导史瓦西方程的方式来处理。我们暂时不考虑热发射，专注于散射;热发射项将被放回第5.5节。

为了更好地理解散射通量的去向，可以考虑垂直方向上厚度为dr*的盒子的能量收支，如图5.2所示。由于辐射场与水平尺寸无关，从侧面进入盒子的通量与从侧面离开盒子的通量是相同的，并且不影响预算。如果盒子底部的面积为A，则A■I(t*) cos 0从底部进入盒子，而A■I(0, t* + dr*) cos 0从顶部离开盒子。取其差值，就得到了光束在单位时间内由于散射和吸收而损失的能量。使用公式5.6，这可以简单地写成A■I(0, t*)dr*;在这个表达式中，I是在dr*还是t* + dr*处被求值并不重要，因为dr*被假定为很小。单位时间内分散并重新分配到各个方向的能量为A■woI(0, t*)dr*。现在，为了写出通量的垂直分量在t *和t * + dr *之间如何变化的方程，我们需要找出有多少通量被添加到方向(0)上，由所有其他方向的辐射散射撞击到层上。我们可以通过考虑入射辐射一次一个方向，然后求和。假设一束光沿方向(0')运动，亮度I(0'，^'，t*)。方向(0)的散射来自于图5.2所示阴影平行四边形中的散射体，它比矩形框中的散射体数量大1/ cos 0。此外，从平行四边形的内容中散射出来的辐射只有一部分进入(0，^>)方向，我们将这个比例写为P/4n，其中P取决于入射方向和散射方向。因此，散射对方向(0)的辐射贡献为A■(P/4n)woI(0'，^'，t*)dr*/cos0，其垂直分量通过乘以cos0得到A■(P/4n)woI(0'， t*)dr*。这是由散射贡献的垂直通量，并被添加到离开盒子顶部的通量中。散射作为方向(0，添加到公式5.6的右边)的辐射源。将盒子底部的面积分开，盒子的通量平衡为dI(0,4 >) cos 0 = - I(0， ^)dr* + - P(0,0 '， 4>')I(0'， ^')dr* (5.7)

如果只考虑单个方向(0'，)散射所贡献的通量，则为4n。为了完成方程，必须对所有入射角(0')积分。为了确定辐射场的完全一般性，必须同时满足每个传播方向的通量平衡。在朝着这个目标前进之前，我们将检查公式5.7，以验证散射能量是守恒的。将控制体积草图应用到入射光束方向，我们推断入射光束沿(0'方向运动，以I(0'， ^')dr*(每单位面积)的速率在控制体中沉积能量。其中woP/4n的比例应该表现为盒子中能量沿(0)方向传播的增加，这正是Eq 5.7中出现的源项。

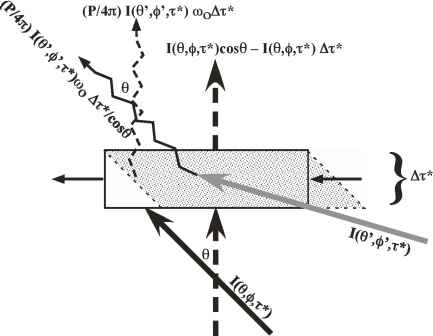
图5.2:散射控制体积，表示入射光束在(0’方向上的散射所增加的通量，仅考虑厚度为dr*的平板的贡献。入射光束照亮了整个平板，但只有阴影平行四边形中的散射体对(0，^>)方向的散射辐射有贡献。实线波形线表示散射辐射，虚线波形线表示散射通量的垂直分量。垂直的直线虚线箭头给出了(0)方向上通量的垂直分量，并显示了它在板坯穿过时的变化情况。由于吸收和散射，通量从(0，光束损失。由于散射而损失的通量在所有其他方向上表现为散射辐射;这些在图中没有显示出来。

值得仔细思考图5.2，因为在这种计算中出现的余弦项——也是编写双流近似时大多数困难的来源——可能相当令人困惑。余弦权值起着两个完全不同的作用。在一种伪装下，它们表示沿倾斜路径遇到的散射体或吸收体的数量，但在另一种伪装下，它们表示通量在垂直方向上的投影。大多数困惑可以通过认真思考控制体积的能量预算来解决。

图5.2中引入的量P称为相位函数，描述了散射辐射在各个方向上的分布情况。对于球对称散射体，相位函数仅取决于入射光束与散射光束之间的角度©(如图5.1所示)。相位函数通常表示为cos©的函数。设fi[为入射光束传播方向的单位向量，fsca为某散射辐射传播方向的单位向量，则其中0和$为入射光束的方向角，0'和为所考虑的散射光束的角度。介质整体的相位函数可以从进行散射的单个粒子的相位函数中确定——记住，从和dr*中，我们已经知道从一束散射出去的能量的量，所以相位函数只需要告诉我们能量如何在各个方向上分布。单个粒子的相位函数是这样定义的:在方向(0'，$')附近的立体角d£l'元素内的散射通量为XsCaI(0,4 >)P(cos©(0,0 '，4>'))d£l' / 4n。P被归一化，使得J" pdd = 4n，因此对所有固体角度上的散射通量进行积分得到xscaI。进一步注意，没有明确指定极限的实心角积分表示对整个球的积分。最后的等式是定义的问题，其他两个等式也同样存在，因为如果对整个球积分，可以自由旋转坐标系，以定义与任何选定轴的角度。各向同性散射，其中散射辐射在各个角度上均匀分布，定义为P = 1。

如果大气中的散射体都是相同的粒子，那么介质的相位函数就与单个粒子的相位函数相同。如果一个粒子与另一个粒子的相位函数不同，那么介质的相位函数就是单个粒子相位函数的平均值，与公式5.3兼容加权。当粒子是非球形时，平均是特别重要的。虽然任何单个粒子的相位函数不是cos©单独的函数，但粒子通常是随机方向的，随机方向粒子的集合的平均相位函数就像等效球的相位函数一样。

如果将Eq 5.7除以dr *，并对所有入射方向(0'，$')进行积分，则发现辐射沿(0，方向运动的通量的垂直分量方程，其中cos©以(0,0 '，$-4>')的形式由Eq 5.8给出。热发射会在右边增加一个额外的源项B(v, T(T *))，但我们现在先不考虑它。这是完整的方程它的解给出了辐射场。积分偶联cos的所有方向©= fi[•nsca = cos 0 cos 0' + sin0 sin 0' cos(^ - 4>')

传播;例如，如果用100个角的和来近似积分，这个方程就相当于解了100个耦合常微分方程的方程组。虽然使用现代计算机，这并不像它曾经看起来那样是一项艰巨的任务，但在典型的气候计算中，这仍然是一项棘手的任务，即在辐射-对流模型的每个时间步中，对大量波数中的每个波数进行计算，也许还需要对一般环流模型中的每个纬度和经度网格点进行计算。raybet雷竞技最新此外，如果一个人的目标是理解而不仅仅是计算一个数字，那么手中有一个简化的表格总是有帮助的。因此，我们的重点是将方程简化为两种辐射流的近似方程集，这两种辐射流可以被认为是向上和向下的辐射流。在本节中，我们将导出一些精确的约束，用于获得5.5节中问题的两个流闭包。

我们首先需要定义向上和向下的通量，它们是

通量是这样定义的，两者都是正数。假设dQ可以写成dcos0•d^，那么把所有的通量写成cos0的函数就很方便了，就像我们在这里做的那样。从今往后，我们将分别用Q+和Q-来表示向上半球和向下半球的积分。根据这些定义，净垂直通量(正向上)为I+ - I_ = JIcos 0dQ，对整个球面积分。

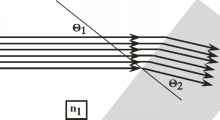
太阳辐射以几乎平行的辐射束的形式进入大气层的顶部，其特点是具有本质上独特的传播角度。它通过散射逐渐转化为辐射，并在各个角度上连续分布。由于入射太阳辐射的角度分布集中在一个传播方向上，因此将辐射分为恰好沿该方向传播的直束分量和在所有角度传播的漫射分量是有用的。在晴朗的天空中，你可以看到太阳是一个轮廓清晰的圆盘，这表明太阳的直束辐射并没有完全通过散射转化为弥散辐射，除非是在多云的情况下。为了定义直束通量，设Lq为太阳常数，Z为垂线与指向太阳的直线之间的夹角;Z称为天顶角。按照惯例，天顶角被定义为指向太阳的矢量的角度，而不是来自太阳的光线的方向。因此，如果0dir是我们通常的角度坐标系中直接光束辐射的角度，天顶角就是Z = n - 0dir。直射光束辐射的方位角^dir是在通常的坐标系中定义的。

现在，由于直束通量集中在一个方向上，基本上任何散射通量都不可能返回到精确的直束方向。这就像在飞镖靶上精确地击中一个无限小的点。因此，通量从直接光束中散射出去，但从未加入其中，并且直接光束呈指数衰减。利用倾斜路径，直接光束通量为Lq exp(- (r^ - t*)/ cos Z)。我们将通量重写为扩散分量和直接光束的和:

我(因为0 = Idiff(因为0,+ Lq exp (- t (t ^ - *) / cos Z) 6 (0 - (n - Z ^害怕r) (5.12)

其中，Idiff是扩散通量，6是狄拉克函数。从现在开始，为了节省符号，我们将在弥漫辐射上去掉“diff”下标，而简单地将弥漫分量写成I。在典型情况下，top-of-atmosphere边界条件规定，所有向下方向角度的散射分量的亮度必须消失。

代入Eq 5.10，漫射通量方程变为- I (cos 6， <) cos 6 = - I (cos 6， <) + - f P (cos 0)I (cos 6'， <')dQ'

dT * ^ 4nJ (5.13)

+ Lq P(cos 0(- cos Z, cos 6，< -

来自直接光束的散射作为漫射辐射的源项。对所有角度积分得到以下精确的净垂直漫射通量的表达式dd* (I+ - I_) = -(1 - -o)J I (cos 6'，<')dfi' + - ole exp (-(t* - t*)/cos Z) (5.14)

since / P(cos0)dQ = 4n。在这个表达式中，I+和I-现在只表示通量的扩散部分。保守的散射-即没有吸收的散射-定义为- o = 1。对于保守散射，方程5.14右边的第一项消失。对直接光束项对t*积分只需乘以cos Z，得到I+ -I- - lqcosz exp(-(t* - t*)/cos Z)是常数。因此，对于保守散射，直接光束垂直通量的总和-这是负的，因为它是向下的-与扩散通量无关的高度。当直接光束耗尽时，损失的通量完全进入漫反射分量。这是应该的，因为在保守散射中，失去的通量没有其他地方去。

式5.14提供了推导双流近似所需的两个约束条件中的第一个。第二个约束条件是将Eq 5.13乘以上下半球之间反对称的函数H(cos 6)，然后进行角度积分。乘以一个反对称函数的基本原理是，我们已经从第一个约束中知道了关于I+ - I-的一些信息，通过反对称函数进行加权，我们得到了关于i++ I-的一些信息。乘以H，进行角度积分，得到

d* JI (cos 6， <)H (cos 6) cos 6dQ = -J IH (cos 6)dQ + -o J G(cos 6')I (cos 6'， <')dQ'

在哪里

G(cos 6') = -1 J H(cos 6)P(cos 0(cos 6, cos 6'， cos <))dQ (5.16)

我们可以用cos <来代替这个表达式中的cos(< - <')，因为积分是对所有角度<的积分，所以方位角的恒定移动不会改变积分的值。由于假定H是反对称的，函数G(cos 6')描述了以6'角入射的光束的上下不对称散射。cos0的对称性意味着G(- cos6 ') = -G(cos6 ')。

习题5.2.1推导G的反对称性。

如果相位函数满足P(cos0) = P(-cos0)，则称散射是对称的。对于对称散射体，前后方向的散射没有区别。从公式5.8可以得出，cos 0(cos 6, cos6 '， <) = -cos 0(- cos6, cos6 '， < + n)。H(cos 6)的反对称性意味着，如果P是对称的，G就消失了，因为(cos6，<)对积分的贡献抵消了(-cos6， + n)的贡献。对于对称散射，公式5.15采用了一种特别简单的形式，因为与-o成比例的两项都消失了。这一结果的物理内容是，对称散射并不直接影响扩散辐射的非对称成分，因为等量的散射向向上和向下的方向。

当散射不对称时，涉及G的项不会消失，我们需要一种方法来描述相函数的不对称。最常见的不对称测量方法是相位函数的余弦加权平均

2 Jcose=-i这就是不对称因子的名称。对称散射的不对称性因子消失。在g = -1的极限下，所有的辐射都是后向散射的，就好像散射的粒子是小镜子一样。当g = 1时，完全没有后向散射，所有的射线都继续向前，尽管它们的运动方向被粒子改变了，就像它们是小透镜一样。

不对称因子g表征了相对于入射光束运动方向的前后向散射不对称，但通过对公式5.8进行一些繁琐的操作，可以表明，无论入射光束的方向如何，相同的因子表征了向上向下方向的余弦加权不对称。具体来说，如果入射光束的方向为(^'，0')，则

-1 J P(cos©(cos 0, cos 0'， cos cos 0dQ = g cos 0' (5.18))

d^ = d^-d cos 0。如果我们在Eq. 5.15中选择H(cos 0) = cos 0，这将导致一个特别整洁的结果，因为G(cos 0') = gcos 0'，散射方程的反对称投影变成d

——我(因为0 ^)cos2 0 dn = -(1 -外国佬)(I + - I_) + woLegcos Z exp (- t (t ^ - *) / cos Z) (5.19)

出现在左边的积分只对辐射场的对称分量敏感。为了得到双流闭包，必须用i++ I_表示积分，这就需要对辐射的角度分布做一个假设。同样的假设适用于公式5.14的右边，可以用i++ I_来估计J IdQ。我们将遇到的不同形式的双流近似对应于不同的假设辐射度角分布．

对于其他形式的H，不对称函数G(cos 0')具有更复杂的行为，不那么容易描述。我们需要处理的另一种形式的H是f1 (cos0 > 0) H(cos0)=， f0 < 0 (5.20)

I -1对于cos0 < 0，它被用来推导双流方程的半球面各向同性形式。这种选择是方便的，因为Eq. 5.15的左边化简为i++ I_的导数，但它是不方便的，因为G不再是一个简单的余弦依赖于入射角。人们可以简单地从介质的相位函数中计算G，并使用它来形成散射方程中的权重，但考虑到我们已经接受了将问题简化为两个流的不准确性，这几乎不值得付出努力。相反，我们将G近似为具有余弦依赖关系，就像在前面的例子中那样。如果相位函数具有P = 1 - 3 b + a cos©+ b cos2©的形式，则这种近似是准确的，并且可以添加三阶和四阶项，而不会严重影响表示。通过执行定义不对称因子的积分，我们发现g = 1a。然后，为相函数的假设形式计算g，我们发现g = 1a cos 0' = | gcos 0'。由这个结果可以得到反对称散射方程投影

我+ + I_ () = - (1 - 3 g) (I + -我-)+ ^ qlq3gcos Zexp (- t (t ^ - *) / cos Z) (5.21)

如果我们重新定义不对称因子为3g，右边就会与Eq. 5.19完全相同。式5.21已经写成了向上和向下流的形式，不需要进一步的近似，就可以用来推导一个双流近似。为了完成半球面各向同性双流方程的推导，只需使用假定的辐射度角分布，将Eq. 5.14中出现的积分f IdQ写成i++ 1_的形式。如果假设我分别在正向和反向方向上是半球面各向同性的，那么这个积分实际上是2(i++ I_)，这就完成了问题的闭合。

我们还需要定义最后一个基本量，即折射率，它表征了介质对电磁辐射传播的影响。折射率相当于表示散射和吸收截面中已经存在的信息的另一种方式。对于一种广泛的材料——包括所有在行星气候中具有重要意义的材料——电磁辐射在材料中的传播是用与麦克斯韦电磁方程相同的方程来描述的，除了决定传播速度的常数发生了变化(“光速”raybet雷竞技最新)。特别地，方程保持线性，因此波动方程的任意两个解的叠加也是一个解，允许从更基本形式的解建立复杂的解。介质中光速的降低是因为施加波的电场在构成材料的分子中诱导了偶极矩，这反过来又产生了一个电场，这个电场改变了施加波的电场。方程保持线性，因为非奇异材料的感应偶极矩只是与施加的电场成正比。当介质不吸收时，真空中的速度与介质中的速度之比是一个实数，称为折射率。

折射率的物理意义是，在折射率的不连续处，例如悬浮在大气中的云粒子表面，传播速度的跳跃导致击中界面的光的部分反射，以及透射光相对于原始传播方向的偏转(折射)。折射率跳得越大，反射和折射就越大。在相当大的程度上，光在撞击界面时的折射可以用粒子的观点来理解。如果有人将一束平行光束表示为一组在外部介质中以ci速度移动的平行粒子流，那么如果这些流撞击到一个速度为c2 < ci的介质界面，那么先撞击的流将首先减速，这意味着波阵面将倾斜，光束的传播方向将向法线偏转，如图5.3所示。经典的类比是一列列队行进的士兵，他们遇到了泥泞的田地的边缘，这减慢了行军的速度。如果©i是相对于界面法线的入射角，而©2是界面另一侧的折射光束的角度，则由斯涅尔定律描述由于速度变化而产生的偏转，即c2 sin©i = ci sin©2，或等价于sin©2 = (ni/n2)sin©i。现在，如果一束光束以©2的角度在介质中行进，并进入折射率较低的介质(例如玻璃对空气)，那么出射光束的角度为sin©i = (n2/ni)sin©2;因此，光束偏离法线，如图所示。在这样的界面上，如果(n2/ni)sin©2 > 1，则没有透射光束，光线被折射得如此之多，以至于完全反射回介质中

图5.3:一束光在折射率为ni的介质和折射率为n2的介质之间的界面上的折射。在草图中，所以光在介质中的速度比在周围环境中的慢，就像玻璃或空气中的水一样。

——这种现象被称为全内反射。在现实中，界面上总是有部分反射。部分反射，以及我们将遇到的许多其他现象，取决于麦克斯韦方程所描述的光的波动性质，并且不能被“微粒”观点所捕获。对于早期光学理论家来说，这是一个开创性的概念挑战，就像黑体辐射对于主持量子理论曙光的研究人员一样。

折射率的概念可以推广到吸收介质。假设平面波在介质中传播具有空间相关性exp(2nikx)，其中x是在传播方向上测量的距离。然后，波的速度用它的频率和波数表示就成了

Kf，其中c是真空中的光速。因此k = (v/c)n。注意v/c是我们一直用来描述辐射的真空波数。对于实n, k是介质中的波数，它比真空波数大n倍。如果我们允许n为复数，它的虚部表征了介质的吸收特性。要看到这一点，写kn + iki =- ur + i-ni (5.23)

由于波具有空间依赖性exp(2nikx) = exp(wnikkrx) exp(-2nkjx)，系数2nkj = 2nuI(v/c)给出了光在单位行进距离上的吸收衰减。请注意，由于v/c的因素，2nnI给出了光束经过等于一个光波长的距离后的衰减。因此nI = 1对应一个极强的吸收。例如，可见光在这样的介质中传播一下午时，就几乎完全被吸收了。

吸收系数kI与我们在第4章中介绍的每单位质量的吸收截面成正比，在上面粒子吸收的背景下再次出现。如果介质的密度为p，则相应的质量吸收系数为k = 2nkI/p =

	Thermal-IR	近红外线	太阳能	uv - b
液态水	1.40	1.31	1.33	1.43
水冰	1.53	1.29	1.31	1.39
二氧化碳的冰	1.45	1.40	1.41	1.54
液态甲烷	1.28	1.27	1.27	1.49
硫酸38%	1.56	1.36	1.38	1.53
硫酸81%	1.41	1.51	1.44	1.58

表5.1:选定凝聚态物质折射率的实部。热红外数据为600 cm-1，近红外数据为6000 cm-1，太阳数据为17000 cm-1(。59 pm)和50000 cm-1的UV-B(。下午2点)。液态水的数据采集温度为293K，水冰温度为273K，二氧化碳冰温度为100K，液态甲烷温度为112K, H2SO4温度约为270K。后者给出的浓度百分比以重量百分比表示。

(v/c)/p。以mks为单位，这个量的单位是m2/kg，因此是每单位质量的吸收截面。

表5.1给出了一些常见的云形成物质的真实折射率。这些物质和类似物质的折射率大约在1.25到1.5之间，只与波数有微弱的关系;数据还显示，折射率对温度的依赖性很小。折射率对波长的微弱依赖确实引起了许多容易观察到的现象，例如棱镜使颜色分离或水滴形成彩虹，但是这些现象尽管很漂亮，对科学家来说却并不重要行星能量平衡．真实折射率的典型渐变变化的一个例外发生在光谱局部化吸收特征附近;实际指数在这些点附近也有很大的变化。在考虑悬浮在大气气体中的粒子对光的散射时，通常可以将气体的折射率设为单位而不太损失精度。在真空中，n =1，而我们认为密度最大的气体并没有太大差别。具体来说，对于气体n - 1与密度成正比。在293K和1bar处，地球上的空气在可见光谱中的折射率为1.0003。在同样的条件下，二氧化碳的指数为1.0004，即使在金星表面压力为90巴的情况下，其指数也只有1.016。由此产生的大气气体的折射可以通过从可见光到无线电光谱的折射观测来确定大气的性质，但它对云粒子的散射几乎没有影响。

就实际的折射率而言，云是由什么物质构成的似乎无关紧要。表5.1中所见的微小差异远不如云颗粒大小和云中凝结物质质量的影响重要。另一方面，不同物质的吸收特性有很大的不同，这对云层对行星能量收支的影响有深远的影响。液态水、水冰和CO2冰的虚指数的行为如图5.4所示。水和水冰云在地球的大部分地区几乎是透明的太阳光谱；对于这些物质，波数在10000cm-1到48000cm-1之间(波长在1pm到。2pm之间)，nj小于10-6，尽管当人们进入远紫外时，吸收急剧增加。在热红外然而，在光谱中，水和水冰是非常好的吸收剂，在50到1000 cm-1的波数之间，nj大于.1。如此大的nj值意味着当通过直径为10 pm的云粒子时，大部分热红外通量将被吸收。为此，红外散射由水和水-冰云可以安全地忽略，这样的云被视为纯粹的红外吸收器和发射器。但由二氧化碳冰组成的云却不是这样(在早期火星上很重要，也许雪球地球)或液态CH4

(在土卫六上很重要)。除了对远紫外线的强烈吸收外，二氧化碳冰云在太阳光谱中仍然相当透明。相比之下水的云然而，它们对热红外基本上是透明的。对于CO2冰云，在1000 ~ 2000 cm-1之间n/小于10_4，即使在500 ~ 1000 cm_1之间n/也一般小于0.01，只有在600 cm_1附近有一个强而窄的吸收特征。同样，液态甲烷在10和1200 cm_1之间的n/ well低于。001。这两种情况都是红外线散射效应可以对OLR产生重要影响，导致一种新型的温室效应。浓硫酸，构成了地球上的气溶胶和金星上的云，在波数大于4000cm_1时是相当透明的，但在波数较小时，虚折射率会大大增加，在热红外中，硫酸几乎和水一样吸收。尽管如此，硫酸云的散射对金星的OLR有显著的影响，因为金星非常热，在波数大于4000cm_1时有相当大的热发射。

硫酸盐气溶胶的强烈反射特性解释了在图1.17的温度时间序列中看到的对流层的火山冷却，但是什么解释了随之而来的平流层变暖?由于气溶胶在可见光和太阳近红外中大部分是透明的，答案必然在于热红外效应。这似乎是矛盾的，因为我们已经知道，通过添加二氧化碳来增加平流层的红外透明度会使平流层冷却。解决这一矛盾的方法是在二氧化碳和气溶胶吸收光谱的差异中找到的。二氧化碳的吸收和排放非常有选择性，我们在第四章中看到，这导致平流层温度比灰色身体的皮肤温度低得多。相比之下，硫酸盐气溶胶的作用更像一个灰色的物体。因此，它们将平流层温度提高到接近灰色身体皮肤温度的水平。任何广泛吸收热红外的气溶胶都应该有类似的行为。

一般的经验法则是，典型的成云凝析液在可见光和近紫外波段非常透明，在近红外波段相当透明，但在热红外波段的吸收特性有很大差异。大多数物质——无论是气态的还是凝聚态的——都是紫外线光谱中波长低于0.1 ^m的短波部分的很好的吸收剂。因此，这部分紫外线光谱通常被称为“真空紫外线”，因为它基本上只存在于外层空间的硬真空中。

继续阅读:分子散射瑞利散射

这篇文章有用吗?

基本概念

相关的帖子