马赫数

图8.3:**标题

能量曲线通过声速点的运动意味着M(r)和w(r)的梯度在那里有平方根奇点——这是违反跨声速规则的结果。从物理的角度来看，重要的不是奇点，而是这样一个事实:一旦r超过音速点，解就完全不存在了。

对式8.32的检验表明，温度随着声速点的接近而降低;这通过降低声速来增加马赫数。事实上，在马赫数小到动能可以忽略不计的情况下，能量方程简化为干静态能量守恒cpT + gz，并告诉我们大气沿干绝热线上升。这意味着它不能上升很远，因为对于干绝热层来说，在一个有限的高度，温度会降至零度。动能项的加入使大气在温度降至零度之前就耗尽了能量。如果我们试图从一个现实的基础温度开始，使大气从水动力上逃逸，这就是我们所要对抗的情况:如果没有一些额外的能量供应，大气在走得很远之前就会耗尽能量。在这种情况下，能量学要求大气在没有平均流出的情况下进入静止状态。当从具有类似地球引力的行星上的低温开始时，能量必须沉积在上层气氛井然有序让它逃脱。一般来说，这种能量以极紫外线的形式提供。

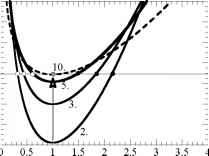
接下来，我们将研究在满足跨音速规则和绝热流体动力逸出可能的情况下能量曲线的几何形状。情况如图8.4所示。为了从亚音速过渡到超音速状态，能量曲线首先上升到亚音速和超音速溶液在音速点的结合处，但随着r的进一步增加，能量曲线再次向下移动，使溶液继续在超音速分支上运行。跨声速规则相当于这样的要求:当以r的函数表示时，能量曲线E(M = 1, r/ro)的最小值在r = rc处有最大值，因此曲线先上升到声速点，然后再掉头向下。

通过使用E(M = 1,r/ro)的表达式来验证这个性质，并通过对r求导来确定其最小值。为了简单起见，你可以将注意力限制在绝热情况0 = const..

1.5 2 2.5马赫数

1.5 2 2.5马赫数

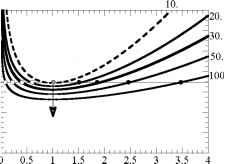
图8.4:r/rs = 10满足跨声速规则时的能量曲线序列左图:随着r/rs从2增加到10，能量曲线向上移动。右图:随着r/rs从10进一步增加到100，能量曲线向下移动。

EUV加热驱动逸出

现在是时候把加热问题考虑进来了。加热从两个方面改变了前面的结构:首先，表达式E不再独立于r，而是由于太阳辐射或其他来源的能量沉积而变化。这使得能量曲线随r上下移动，而不改变其形状。其次，加热会使0随r变化，从而改变能量曲线的形状。然而，任何r的能量曲线在马赫数为单位时都有一个唯一的最小值，为了实现从亚音速到超声速流动的转变，定义任意给定r的可用能量量的直线必须高于最小值，并在最小值处切线(要么向上移动曲线，要么向下移动直线，或者两者结合)。然后随着r的进一步增加，将这条定义可用能量的线移动到比最小值更高的距离。

为了将加热纳入能量方程，我们将方程8.28右侧的非绝热项改写为:

dr pSQ/dt pdr/dt

其中q是单位体积的升温速率。现在设F(r)为能量的通量由于其他手段，而不是大流体流动，惯例，向内的通量是正的。我们将主要处理辐射通量，但F同样可以很好地表示由于分子扩散热量。在通量方面，加热速率由q常数给出，能量方程中的加热项就变成了

r2d (r2F)/dr，已知$是

由于这是通量的梯度，式8.28告诉我们，它可以与前面的E的表达式结合起来，得到修正的守恒定律

1 2 I rp K rs r2 F

-u) + cpT——2gsrs——= Eo

其中Eo是常数。注意F/$是能量通量除以质量通量，因此有速度平方的维度。对于能量通量的给定变化，降低质量通量$将导致能量密度E(方程中的第一对项)的更大径向变化，因为流体在缓慢移动时有更多的时间积累能量。

加热的辐射部分的处理有点棘手。在我们之前的计算中行星的温度在美国，我们正在做一个全球平均能源预算，假设全球大气条件一致。这需要计算出被地球大气层拦截的EUV通量的数量，并将其均匀分布在球体上。太阳热量在外层大气上的有效重新分配的假设是非常值得怀疑的，但这在水动力逃逸计算中是相当常见的，而且在任何情况下，这是唯一的近似值，使我们能够在不进行非常广泛和复杂的数值模拟的情况下取得进展。尽管如此，还有一个在我们之前处理全球平均能源预算时没有出现的额外问题。像往常一样，行星拦截了一个半径一定的光盘，拦截的通量均匀地分布在相应半径的球体表面。目前情况的不同之处在于，大气层的密度足以吸收大量的EUV辐射，可以将许多行星的半径从表面延伸出去。因此，被拦截辐射的圆盘的半径取决于大气的光学厚度(即密度)。让我们假设大气层对EUV是透明的在半径远于半径的范围内，但是更近的大气层吸收强烈。那么，如果Fq是EUV从太阳入射的通量(类似于太阳常数)，则拦截功率为nr2bsFQ。如果我们希望这是进入系统的总功率，那么对应的均匀径向通量4nr2F(r)通过半径为r的壳必须保持在值nr2absFQ为r >拉布。 Therefore, we model radiative absorption by stipulating that r2F(r) = 1 r2absFQ for r > rabs while allowing the flux to decay to zero as radiation is absorbed deeper in the atmosphere.

式8.36对给定加热水平所能维持的质量通量施加了强有力的约束。我们像往常一样假设逃逸大气底部的w很小，但这次我们还假设底部是凉爽的，所以cpT与底部的引力项相比可以忽略不计。这是典型的情况，在这种情况下，大气受到强烈的引力束缚，逃逸参数Xc很小。与绝热逸出的情况不同，我们没有赋予大气底部足够的热能来维持外流，而是通过吸收恒星通量逐渐将其沉积下来，通常是在极紫外光谱中。在基底(辐射通量降为零的地方)和无穷远处相等的能量可以得到这个关系

$(4% Fq) = 2 wL + hgsrs ^ (8.37)

由于w2 > 0，对于任何给定的辐射吸收量，这强加了质量通量$的上界。请注意，在通量项中加入热扩散后，这种能量约束仍然存在，因为扩散只是在垂直方向上重新分配能量，而不会向系统添加新的能量。如果(rabs/rs)2«1和rs/rb«1是典型的情况，那么约束就是$ < 1 F(.^，/gsrs. 1)。重要的是要认识到，逃逸通量的这个界限只适用于低温极限，在低温极限中，与重力势相比，底部的cpT可以忽略不计。对于任何有限的温度，逸出通量可以超过极限通量，超出的量随着温度的升高而增加。当基底温度接近绝热逸出可能的温度时，逸出通量可以变得任意大，只受基底密度的限制。

约束的物理内容很简单:逃逸大气携带动能和势能，这种向外的能量通量必须与逃逸大气内吸收的辐射能供应相匹配。从的观点来看，由于质量流而逸出的能量通量可以忽略不计行星能量平衡；到目前为止，能量损失仍然主要由红外发射．然而，仅从外层大气的能量预算的角度来看，由于质量流出造成的能量损失可能是主要的项-至少对于像H2这样的红外发射器较差的气体来说是如此。红外发射，就其发生的程度而言，可以被认为是从可用于维持逃逸的EUV加热供应中窃取能量。

为了完成解，我们需要知道势温随半径的变化。一旦势温已知，我们就有足够的热力学信息来计算压强和密度的分布。势温的径向变化由熵方程得到:

d 1¿q 1 ^q/dt 1 (r/rs)2Q

drcpln 0 = Tdr = t^ = t (8.38)

加热项(r/rs)2Q可以像以前一样写成通量的径向梯度，但由于熵方程中出现了因子1/T，这个方程不能像我们计算能量那样积分得到熵和通量之间的点关系。点r^和rB之间的熵变取决于两点之间的加热曲线的形状，而不仅仅是增加的热量;低温加热量比高温加热量对熵的影响更大。

现在我们将展示一些数值解的情况下，其中加热Q是一个已知的函数r。辐射加热取决于密度和温度所以严格地说，它必须和大气结构；一旦理解了如何解决更简单的问题，这种情况的扩展就很简单了。在给定加热条件下，数值求解如下。首先选择临界点位置rc/rs，从中可以计算出临界点声速和温度。然后，将微分方程8.38朝着行星的方向积分。由于转义通量$在这个方程中作为参数出现，因此必须猜测$的值才能进行积分。$的值也固定了临界点的密度，因为临界点的速度是局部声速。在公式8.38的每一步积分中，都得到ln 0的值，但要继续，还需要更新t的值。这是通过求解能量方程8.36(用公式8.33重写为马赫数)的马赫数来完成的，马赫数遵循亚音速分支。马赫数反过来又决定了新的温度，并允许积分进一步进行。随着积分的进行，可能会遇到一个点，在这个点上，能量方程的解不再存在，在这种情况下，所选择的$值是不可实现的。 If this situation doesnt arise, the integration is continued until the base rb is reached. One now knows the value of 0 there, which for positive heating will be less (usually much less) than the value at the critical point. The integration has already completely determined the temperature大气结构， rb处的势温与rc处的值之比决定了rb处的密度与rc处(已知)密度之间的比例常数。这个过程产生一系列解，以rc和$作为参数。当$较大时，式8.38表示潜在温度为常数，在这种情况下，我们恢复绝热逃逸解，通常在底部具有非常高的温度。随着$变小，加热使底部的潜在温度远小于临界点的潜在温度，这就导致底部的温度较低。然而，当$设置得太小时，温度就会被驱动到过低的值，在某一点上，在不满足跨声速规则的半径处会出现超音速转变，这时解就不复存在了。这一过程只需要对一阶微分方程进行积分，并利用牛顿法求解每一步的能量方程。它的实现非常简单。

在展示使用上述过程获得的特定解之前，确定一些相关的无量纲参数是有用的。前面确定的能量有限的逸出通量为$的无量纲化提供了一个方便的尺度。我们称极限通量为$*。可以写成2Fq/w"^sc，其中wesc为表面逃逸速度，即^J2gsrs。我们可以定义一个特征温度T*，使得cpT* = w\sc。加热可以写成Q = (d/dr)(r2/r2sF)，所以它可以通过将熵方程两边乘以rs(相当于以行星半径为长度单位)，然后写成F = Fq■(F/Fq)如果温度对T*是无量纲化的，那么熵方程只依赖于EUV通量、逃逸速度和逃逸通量，通过无量纲组合$/$*。具体来说，无量纲熵方程变成了dln 0 =1 ^ (8.39)

继续阅读:太阳风侵蚀

这篇文章有用吗?

0 0